
| 2 |
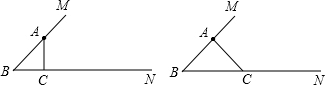
| ||
| 2 |
| 2 |


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
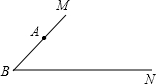
 如图所示,∠MBN=45°,若△ABC的顶点A在射线BM上,且AB=
如图所示,∠MBN=45°,若△ABC的顶点A在射线BM上,且AB=| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
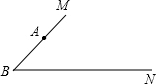
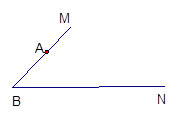
(12分)如图所示,∠MBN=45°,若△ABC的顶点
A在射线BM上,且AB=![]() ,点C在射线BN运动(C
,点C在射线BN运动(C
不与B重合).请你探究:
(1)当BC= 时,△ABC是直角三角形,并标出所有符合要求的C点;
(2)当BC的值在 范围时,△ABC是锐角三角形;
 (3)当BC的值在 范围时,△ABC是钝角三角形 .
(3)当BC的值在 范围时,△ABC是钝角三角形 .
查看答案和解析>>
科目:初中数学 来源: 题型:

 ,点C在射线BN运动(C
,点C在射线BN运动(C查看答案和解析>>
科目:初中数学 来源:2011年江苏省邳州市运河中学八年级(上)期中测试数学卷 题型:解答题
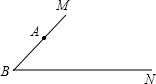
(12分)如图所示,∠MBN=45°,若△ABC的顶点
A在射线BM上,且AB= ,点C在射线BN运动(C
,点C在射线BN运动(C
不与B重合).请你探究:
(1)当BC= 时,△ABC是直角三角形,并标出所有符合要求的C点;
(2)当BC的值在 范围时,△ABC是锐角三角形;
(3)当BC的值在 范围时,△ABC是钝角三角形 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com