
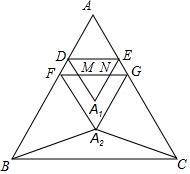
 如图,已知等边△ABC中,DE∥BC,FG∥BC,现将等边△ABC分别沿DE和FG对折,点A分别落在点A1和点A2,连接A2B,A2C.
如图,已知等边△ABC中,DE∥BC,FG∥BC,现将等边△ABC分别沿DE和FG对折,点A分别落在点A1和点A2,连接A2B,A2C.分析 (1)由△A2FG是等边三角形,得出A2F=A2G,∠A2FB=180°-∠AFG-∠A2FG=60°,同样,求出∠A2GC=60°,所以∠A2FB=∠A2GC,FB=AB-AF=AC-AG=GC,根据SAS得出△A2FB≌△A2GC,从而A2B=A2C;
(2)①由FG∥BC得出∠AFG=∠ABC=60°,∠AGF=∠ACB=60°,由等边三角形的判定方法可以得出△AFG是等边三角形,结合对折的性质写出剩余的4个等边三角形;
②首先推出△A1MN是等边三角形,那么求△A1MN的周长,关键就是求其边长,根据对称性,可以得出.
解答 解:(1)证明:∵是△ABC等边三角形,
∴∠A=∠ACB=∠ABC=60°,AB=AC.
∵FG∥BC,∠AFG=∠ABC=60°,
∴△AFG是正三角形.
由对折可知,△AFG≌△A2FG,
∴△A2FG是正三角形.
∴A2F=A2G,∠A2FB=∠A2GC=60°.
又∵AF=AG,
∴BF=CG.
∴△A2FB≌△A2GC,
∴A2B=A2C.
(2)①图中除等边△ABC外还有7个等边三角形,理由如下:
∵等边△ABC,
∴∠A=∠ACB=∠ABC=60°,AB=AC.
∵FG∥BC,∠AFG=∠ABC=60°,
∴△AFG是等边三角形,
由对折的性质推知:△A2FG是等边三角形,
同理:△ADE、△A1DE、△A1MN是等边三角形.
∵∠DFM=∠DMF=60°,
∴△DFM是等边三角形,
同理△ENG是等边三角形.
综上所述,图中除等边△ABC外还有 7个等边三角形;
故答案是:7;
②∵∠A1MN=∠A1NM=∠MA1N=60°,
∴△A1MN是等边三角形.
又∵DE=$\frac{7}{3}$cm,FG=4cm,△DFM是等边三角形,
∴MD=FD=4-$\frac{7}{3}$=$\frac{5}{3}$.
∴MA1=A1D-MD=$\frac{7}{3}$-$\frac{5}{3}$=$\frac{2}{3}$(cm).
∴△A1MN的周长为2cm.
故答案是:2.
点评 本题考查几何变换综合题,需要掌握图形的折叠变化及等边三角形的性质和判定.关键要理解对折是轴对称,根据轴对称的性质,对折前后图形的形状和大小不变,只是位置发生变化.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4 个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
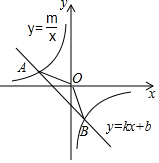 如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | 1 | C. | -5 | D. | -1.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com