
 如图,△ABC中,∠ACB=90°,AB=5,BC=3,CD⊥AB,则CD长为$\frac{12}{5}$.
如图,△ABC中,∠ACB=90°,AB=5,BC=3,CD⊥AB,则CD长为$\frac{12}{5}$. 分析 首先根据勾股定理求得直角三角形的第三边,再根据直角三角形斜边上的高等于两条直角边的乘积除以斜边即可.
解答 解:∵△ABC是直角三角形,AB=5,BC=3,
由勾股定理有:AC2=AB2-BC2.
∴AC=$\sqrt{{5}^{2}-{3}^{2}}$=4.
又∵S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$BC•AC,
∴CD=$\frac{AC•BC}{AB}$=$\frac{12}{5}$;
故答案为:$\frac{12}{5}$.
点评 本题考查了勾股定理以及三角形面积的计算;熟练运用勾股定理,特别注意:直角三角形斜边上的高等于两条直角边的乘积除以斜边.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:选择题
| A. | (-4)2>(-3)2 | B. | |-4|>|-3| | C. | -4>-3 | D. | $-\frac{1}{4}$>$-\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,同一时刻在阳光照射下,树AB的影子BC=3m,小明的影子B'C'=1.5m,已知小明的身高A'B'=1.7m,则树高 AB=3.4m.
如图,同一时刻在阳光照射下,树AB的影子BC=3m,小明的影子B'C'=1.5m,已知小明的身高A'B'=1.7m,则树高 AB=3.4m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
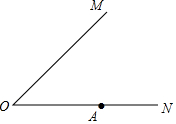 已知:如图,∠MON及边ON上一点A.在∠MON内部求作:点P,使得PA⊥ON,且点P 到∠MON两边的距离相等.(请用尺规作图,保留作图痕迹,不要求写出作法,不必证明).
已知:如图,∠MON及边ON上一点A.在∠MON内部求作:点P,使得PA⊥ON,且点P 到∠MON两边的距离相等.(请用尺规作图,保留作图痕迹,不要求写出作法,不必证明).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 二次函数y=ax2+bx+c(a≠0)图象如图示,下列结论:
二次函数y=ax2+bx+c(a≠0)图象如图示,下列结论:| A. | ①④ | B. | ②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com