
分析 本题中到电脑公司刻录需要的总费用=单价×刻录的数量,而自刻录的总费用=租用刻录机的费用+每张的成本×刻录的数量.列出总费用与刻录数量的关系式,然后将两种费用进行比较,看看不同情况下自变量的取值范围,然后判断出符合要求的方案.
解答 解:设需刻录x张光盘,则
到电脑公司刻录需y1=4x(元),
自刻录需y2=60+2x(元),
∴y1-y2=2x-60=2(x-30),
∴当x>30时,y1>y2;当x=30时,y1=y2;当0<x<30时,y1<y2.
即当这批光盘多于30张时,自刻费用省;当这批光盘少于30张时,到电脑公司刻录费用省;当这批光盘为30张时,到电脑公司与自刻费用一样.
点评 本题主要考查了一次函数的应用,根据题意列出总费用和刻录光盘数量的函数式是解题的关键.


科目:初中数学 来源: 题型:解答题
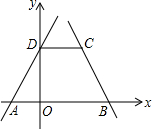 一次函数y=2x+2图象与x轴、y轴分别交于A、D两点,一次函数y=-2x+8与x轴交于B点,过D点作DC∥x轴,交直线y=-2x+8于点C.
一次函数y=2x+2图象与x轴、y轴分别交于A、D两点,一次函数y=-2x+8与x轴交于B点,过D点作DC∥x轴,交直线y=-2x+8于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
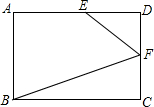 已知:E、F分别是矩形ABCD的边AD、CD上一点,且DF=CF,∠DEF=2∠CBF.若AB=4,BC=6,则AE=$\frac{10}{3}$.
已知:E、F分别是矩形ABCD的边AD、CD上一点,且DF=CF,∠DEF=2∠CBF.若AB=4,BC=6,则AE=$\frac{10}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
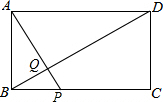 如图,矩形ABCD中,AB=4,BC=10,点P为BC边上一动点,AP交BD于点Q.点P从B点出发沿BC边以每秒1个单位长度的速度向C点移动,移动时间为x秒.设S△AQD+S△PQB=y,写出y与x之间的函数关系式,并探究P点运动到第几秒与第几秒之间时,y取得最小值.( )
如图,矩形ABCD中,AB=4,BC=10,点P为BC边上一动点,AP交BD于点Q.点P从B点出发沿BC边以每秒1个单位长度的速度向C点移动,移动时间为x秒.设S△AQD+S△PQB=y,写出y与x之间的函数关系式,并探究P点运动到第几秒与第几秒之间时,y取得最小值.( )| A. | 3到4 | B. | 4到5 | C. | 5到6 | D. | 6到7 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
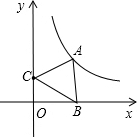 如图,点A是反比例函数y=$\frac{5\sqrt{3}}{x}$(x>0)图象上一点,点B是x轴正半轴上一点,点C的坐标为(0,2),当△ABC是等边三角形时,点A的坐标为($\frac{3\sqrt{3}}{5}$,$\frac{25}{3}$).
如图,点A是反比例函数y=$\frac{5\sqrt{3}}{x}$(x>0)图象上一点,点B是x轴正半轴上一点,点C的坐标为(0,2),当△ABC是等边三角形时,点A的坐标为($\frac{3\sqrt{3}}{5}$,$\frac{25}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com