
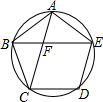
 如图所示,正五边形ABCDE的对角线AC和BE相交于点F,求证:AC=AB+BF.
如图所示,正五边形ABCDE的对角线AC和BE相交于点F,求证:AC=AB+BF. 分析 运用圆周角定理,∠ABE=∠BAC,∠CBE=72°,即可根据等角对等边证明AF=BF,BC=CF,即可解决问题.
解答 解:∵⊙O是正五边形ABCDE的外接圆,
∴∠CBE=$\frac{1}{2}$×$\frac{2}{5}$×360°=72°.
∵⊙O是正五边形ABCDE的外接圆,
∴∠BAC=∠ABE=$\frac{1}{2}$×$\frac{1}{5}$×360°=36°,
∴AF=BF,
∠BFC=∠ABE+∠BAC=72°,
∴∠CBE=∠BFC,
∴BC=CF;
同理可证:∠PBC=∠PCB=36°,
∴AC=AF+CF=AB+BF.
点评 该题主要考查了正多边形和圆的关系及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.


科目:初中数学 来源: 题型:解答题
 如图所示,有一根直立标杆,它的上部被风从B处吹折,杆顶C着地离杆底2米,修好后又被风吹折,因新断处D比前一次低0.5米,故杆顶E着地比前一次远1米,求原标杆的长度?
如图所示,有一根直立标杆,它的上部被风从B处吹折,杆顶C着地离杆底2米,修好后又被风吹折,因新断处D比前一次低0.5米,故杆顶E着地比前一次远1米,求原标杆的长度?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 收费方式 | 月使用费/元 | 包时上网时间/小时 | 超时费/(元/分钟) |
| A | 30 | 25 | 0.05 |
| B | 50 | 50 | 0.05 |
| C | 120 | 不限时 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com