
科目:初中数学 来源: 题型:解答题
 如图:已知半圆O的半径为3厘米,半圆A的半径为2厘米,半圆B的半径为1.1厘米,A、O、B在一直线上.﹙π取3.14﹚求:
如图:已知半圆O的半径为3厘米,半圆A的半径为2厘米,半圆B的半径为1.1厘米,A、O、B在一直线上.﹙π取3.14﹚求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
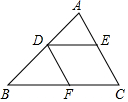 如图,DE∥BC,DF∥AC,则下列比例式中正确的是( )
如图,DE∥BC,DF∥AC,则下列比例式中正确的是( )| A. | $\frac{AD}{DB}=\frac{DE}{BC}$ | B. | $\frac{AE}{EC}=\frac{BF}{FC}$ | C. | $\frac{DF}{AC}=\frac{DE}{BC}$ | D. | $\frac{EC}{AC}=\frac{BF}{BC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平行四边形ABCD中,对角线AC,BD交于O,EO⊥AC,
如图,平行四边形ABCD中,对角线AC,BD交于O,EO⊥AC,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
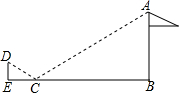 如图,为了测量旗杆AB的高度,小凡在距旗杆底部B点10.8米的C点处放置了一面镜子,当小凡行走到与BC位于同一直线的E点处时,恰好能从镜子中观察到旗杆顶部的A点.已知小凡眼睛所在的D点离地面的高度是1.6米,CE=2.7米,则旗杆AB的高度是( )
如图,为了测量旗杆AB的高度,小凡在距旗杆底部B点10.8米的C点处放置了一面镜子,当小凡行走到与BC位于同一直线的E点处时,恰好能从镜子中观察到旗杆顶部的A点.已知小凡眼睛所在的D点离地面的高度是1.6米,CE=2.7米,则旗杆AB的高度是( )| A. | 6.4米 | B. | 7.2米 | C. | 8米 | D. | 9.6米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读下面的材料:
阅读下面的材料:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com