
【题目】如图,将一块三角板ABC的直角顶点C放在直尺的一边PQ上,直尺的另一边MN与三角板的两边AC、BC分别交于两点E、D,且AD为∠BAC的平分线,∠B=300,∠ADE=150.
(1)求∠BDN的度数;
(2)求证:CD=CE.

【答案】(1)∠BDN=∠CDE=450(2)CD=CE
【解析】试题分析:(1)根据直角三角形的性质,求出∠BAC=60°,然后根据角平分线的性质求出∠CAD=30°,进而根据三角形的内角和求出∠CDA=60°,最后根据角的和差求解即可;
(2)结合(1)的关系,由“等角对等边”得出结论.
试题解析:(1)在直角三角形ABC中,∠ACB=900,∠B=300,
∴∠BAC=600,又AD平分∠BAC,
∴∠CAD=300,又∠ACD=900,
∴∠CDA=600
又∠ADE=150,
∴∠CDE=∠CDA-∠ADE=600-150=450
∴∠BDN=∠CDE=450
(2)在△CED中,∠ECD=900,∠CDE=450
∴∠CED=450
∴ CD=CE


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
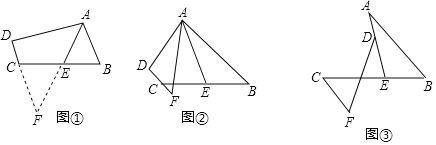
【题目】(1)阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
AB、AD、DC之间的等量关系为 ;
(2)问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
(3)问题解决:如图③,AB∥CF,AE与BC交于点E,BE:EC=2:3,点D在线段AE上,且∠EDF=∠BAE,试判断AB、DF、CF之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芯片是手机、电脑等高科技产品最核心的部件,更小的芯片意味着更高的性能.目前我国芯片的量产工艺已达到14纳米,已知14纳米为0.000000014米,则0.000000014科学记数法表示为( )
A.1.4×10﹣8B.1.4×10﹣9C.1.4×10﹣10D.14×10﹣9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,CE,BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3……
第n次操作,分别作∠ABEn-1和∠DCEn-1的平分线,交点为En.

(1)如图①,求证:∠E=∠B+∠C;
(2)如图②,求证:∠E1=![]() ∠E;
∠E;
(3)猜想:若∠En=b°,求∠BEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y与x的部分取值满足下表:
![]()
(1)试猜想y与x的函数关系可能是你们学过的哪类函数,并写出这个函数的解析式.(不要求写x的取值范围)
(2)简要叙述该函数的性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
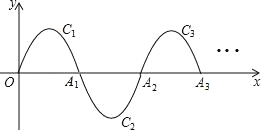
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从某市近期卖出的不同面积的商 品房中随机抽取1000套进行统计,并根据结果绘出如图所示的统计图,请结合图中的信息,解析下列问题:
(1)卖出面积为110~130平方米的商品房 有___套,并在右图中补全统计图.
(2)从图中可知,卖出最多的商品房约占全部卖出的商品房的___%.

(3)假如你是房地产开发商,根据以上提供的信息,你会多建住房面积在什么范围内的住房?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
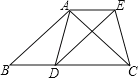
【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:AD=CE;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com