
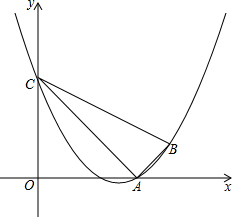
 ��ͼ����֪���κ���y=ax2+bx+3��a��0����ͼ����A��3��0����B��4��1��������y�ύ�ڵ�C������AB��AC��BC��
��ͼ����֪���κ���y=ax2+bx+3��a��0����ͼ����A��3��0����B��4��1��������y�ύ�ڵ�C������AB��AC��BC������ ��1��ֱ�����ô���ϵ�������a��b��ֵ�����ó��𰸣�
��2�����ȵó���OAC=45�㣬�����ó�AD=BD�������DAB=45�㣬���ɵó��𰸣�
��3������������֪�ó�ԲMƽ�Ƶij���Ϊ��2$\sqrt{2}$-$\sqrt{5}$��2$\sqrt{2}$+$\sqrt{5}$�������ó������ߵ�ƽ�ƹ��ɣ����ɵó��𰸣�
��� �⣺��1���ѵ�A��3��0����B��4��1������y=ax2+bx+3�У�
$\left\{\begin{array}{l}{9a+3b+3=0}\\{16a+4b+3=1}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{5}{2}}\end{array}\right.$��
������������ϵʽΪ��y=$\frac{1}{2}$x2-$\frac{5}{2}$x+3��
��2����ABC��ֱ�������Σ�
����B��BD��x���ڵ�D��
��֪��C����Ϊ����0��3��������OA=OC��
���ԡ�OAC=45�㣬
�֡ߵ�B����Ϊ����4��1����
��AD=BD��
���DAB=45�㣬
���BAC=180��-45��-45��=90�㣬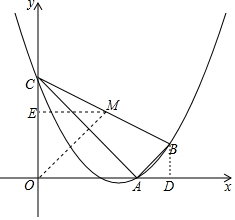 ���ABC��ֱ�������Σ�
���ABC��ֱ�������Σ�
Բ��M������Ϊ����2��2����
��3������
ȡBC���е�M������M��ME��y���ڵ�E��
��M����������2��2����
��MC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$��OM=2$\sqrt{2}$��
���MOA=45�㣬
�֡ߡ�BAD=45�㣬
��OM��AB��
��Ҫʹ������������BA����ƽ�ƣ���ʹ��M1����ԭ�㣬
��ƽ�Ƶij���Ϊ��2$\sqrt{2}$-$\sqrt{5}$��2$\sqrt{2}$+$\sqrt{5}$��
�ߡ�BAD=45�㣬
�������ߵĶ����������¾��ֱ�ƽ��$\frac{2\sqrt{2}-\sqrt{5}}{\sqrt{2}}$=$\frac{4-\sqrt{10}}{2}$����λ����
��$\frac{2\sqrt{2}+\sqrt{5}}{\sqrt{2}}$=$\frac{4+\sqrt{10}}{2}$����λ���ȣ�
��y=$\frac{1}{2}$x2-$\frac{5}{2}$x+3=$\frac{1}{2}$��x-$\frac{5}{2}$��2-$\frac{1}{8}$��
��ƽ�ƺ������ߵĹ�ϵʽΪ��y=$\frac{1}{2}$��x-$\frac{5}{2}$+$\frac{4-\sqrt{10}}{2}$��2-$\frac{1}{8}$-$\frac{4-\sqrt{10}}{2}$��
��y=$\frac{1}{2}$��x-$\frac{1+\sqrt{10}}{2}$��2-$\frac{17-4\sqrt{10}}{8}$��
��y=$\frac{1}{2}$��x-$\frac{5}{2}$+$\frac{4+\sqrt{10}}{2}$��2-$\frac{1}{8}$-$\frac{4+\sqrt{10}}{2}$��
��y=$\frac{1}{2}$��x-$\frac{1-\sqrt{10}}{2}$��2-$\frac{17+4\sqrt{10}}{8}$��
��������������һ��λ�ã�ʹ��M1����ԭ�㣬��ʱ�����ߵĹ�ϵʽΪ��
y=$\frac{1}{2}$��x-$\frac{1+\sqrt{10}}{2}$��2-$\frac{17-4\sqrt{10}}{8}$��y=$\frac{1}{2}$��x-$\frac{1-\sqrt{10}}{2}$��2-$\frac{17+4\sqrt{10}}{8}$��
���� ������Ҫ�����˶��κ����ۺ��Լ����κ�����ƽ�ơ�����ֱ�������ε����ʵ�֪ʶ����ȷ�ó�ԲM��ƽ�ƾ����ǽ���ؼ���


 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��������� | B�� | ���ӻ������ڲ��Ŷ���Ƭ | ||
| C�� | �������ڽǺ�Ϊ180�� | D�� | ����һ��·�ڣ��źŵƸպ��Ǻ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
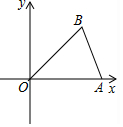 ��ͼ����ƽ��ֱ������ϵxOy�У���֪��A��$\sqrt{2}$��0����B��1��1������ƽ�Ƶ�A����C��ʹ�Ե�O��A��C��BΪ������ı��������Σ�����ȷ��ƽ�Ʒ����ǣ�������
��ͼ����ƽ��ֱ������ϵxOy�У���֪��A��$\sqrt{2}$��0����B��1��1������ƽ�Ƶ�A����C��ʹ�Ե�O��A��C��BΪ������ı��������Σ�����ȷ��ƽ�Ʒ����ǣ�������| A�� | ����ƽ��1����λ��������ƽ��1����λ | |
| B�� | ����ƽ�ƣ�2$\sqrt{2}$-1������λ��������ƽ��1����λ | |
| C�� | ����ƽ��$\sqrt{2}$����λ��������ƽ��1����λ | |
| D�� | ����ƽ��1����λ��������ƽ��1����λ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | ƽ���� | C�� | ���� | D�� | ��λ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | ||
| C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com