
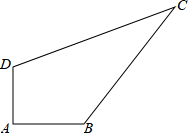
 如图,在四边形ABCD中,AB=4,BC=12,CD=13,AD=3,∠A=90°,求四边形ABCD的面积.
如图,在四边形ABCD中,AB=4,BC=12,CD=13,AD=3,∠A=90°,求四边形ABCD的面积. 分析 先根据勾股定理求出BD的长度,再根据勾股定理的逆定理判断出△BCD的形状,再利用三角形的面积公式求解即可.
解答 解:连接BD.
∵∠A=90°,AB=4,AD=3,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
在△BCD中,BD2+BC2=25+144=169=CD2,
∴△BCD是直角三角形,
∴S四边形ABCD=$\frac{1}{2}$AB•AD+$\frac{1}{2}$BD•BC=$\frac{1}{2}$×3×4+$\frac{1}{2}$×5×12=36.
答:四边形ABCD的面积是36.
点评 本题考查的是勾股定理的逆定理及三角形的面积,能根据勾股定理的逆定理判断出△BCD的形状是解答此题的关键.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
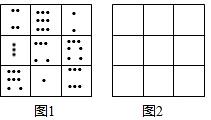 有人建议向火星发射如图1的图案.它叫做幻方,其中9个格中的点数分别是1,2,3,4,5,6,7,8,9.每一横行、每一竖列以及两条斜对角线上的点数的和都是15.如果火星上有智能生物,那么他们可以从这种“数学语言”了解到地球上也有智能生物(人).
有人建议向火星发射如图1的图案.它叫做幻方,其中9个格中的点数分别是1,2,3,4,5,6,7,8,9.每一横行、每一竖列以及两条斜对角线上的点数的和都是15.如果火星上有智能生物,那么他们可以从这种“数学语言”了解到地球上也有智能生物(人).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
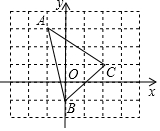 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,3),B(0,-1),C(2,1).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,3),B(0,-1),C(2,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com