
【题目】如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是OB,OD的中点.
(1)试说明四边形AECF是平行四边形.
(2)若AC=8,AB=6.若AC⊥AB,求线段BD的长.

【答案】(1)见解析;(2)4![]()
【解析】
(1)在平行四边形ABCD中,AC与BD互相平分,OA=OC,OB=OD,又E,F为OB,OD的中点,所以OE=OF,所以AC与EF互相平分,所以四边形AECF为平行四边形;
(2)首先根据平行四边形的性质可得AO=CO,BO=DO,再利用勾股定理计算出BO的长,进而可得BD的长.
(1)∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E,F为OB,OD的中点,
∴OE=OF,
∴AC与EF互相平分,
∴四边形AECF为平行四边形;
(2)∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵AC=8,
∴AO=4,
∵AB=6,AC⊥AB,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
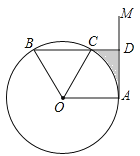
【题目】如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM,垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
(1)求证:AM是⊙O的切线;
(2)若⊙O的半径为4,求图中阴影部分的面积(结果保留π和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件![]() 元,出厂价为每件
元,出厂价为每件![]() 元,每月销售量
元,每月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数:![]() .
.
(1)李明在开始创业的第一个月将销售单价定为![]() 元,那么政府这个月为他承担的总差价为多少元?
元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为![]() (元),当销售单价定为多少元时,每月可获得最大利润?
(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于![]() 元.如果李明想要每月获得的利润不低于
元.如果李明想要每月获得的利润不低于![]() 元,那么政府为他承担的总差价最少为多少元?
元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
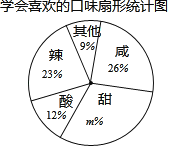
【题目】某初中学校餐厅为了解学生对早餐的要求,随即抽样调查了该校的部分学生,并根据其中两个单选问题的调查结果,绘制了如下尚不完整的统计图表.
学生能接受的早餐价格统计表
价格分组(单位:元) | 频数 | 频率 |
0<x≤2 | 60 | 0.15 |
2<x≤4 | 180 | c |
4<x≤6 | 92 | 0.23 |
6<x≤8 | a | 0.12 |
x>8 | 20 | 0.05 |
合计 | b | 1 |
根据以上信息解答下列问题:
(1)统计表中,a= ,b= ,c= .
(2)扇形统计图中,m的值为 ,“甜”所对应的圆心角的度数是 .
(3)该餐厅计划每天提供早餐2000份,其中咸味大约准备多少份较好?
查看答案和解析>>
科目:初中数学 来源: 题型:
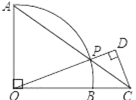
【题目】如图,O为![]() 所在圆的圆心,∠AOB=90°,点P在
所在圆的圆心,∠AOB=90°,点P在![]() 上运动(不与点A,B重合),AP交OB延长线于点C,CD⊥OP于点D.若OB=2BC=2,则PD的长是( )
上运动(不与点A,B重合),AP交OB延长线于点C,CD⊥OP于点D.若OB=2BC=2,则PD的长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
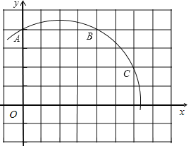
【题目】如图,在平面直角坐标系中,![]() ,则经过
,则经过![]() 三点的圆弧所在圆的圆心
三点的圆弧所在圆的圆心![]() 的坐标为__________;点
的坐标为__________;点![]() 坐标为
坐标为![]() ,连接
,连接![]() ,直线
,直线![]() 与
与![]() 的位置关系是___________.
的位置关系是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
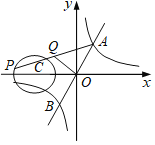
【题目】如图,一次函数y=2x与反比例函数y=![]() (k>0)的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为
(k>0)的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为![]() ,则k的值为( )
,则k的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
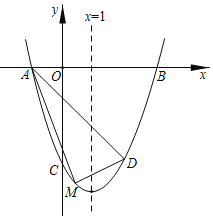
【题目】如图,抛物线y=x2+bx+c与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,﹣3),对称轴为x=1,点D与C关于抛物线的对称轴对称.
(1)求抛物线的解析式及点D的坐标;
(2)点P是抛物线上的一点,当△ABP的面积是8时,求出点P的坐标;
(3)点M为直线AD下方抛物线上一动点,设点M的横坐标为m,当m为何值时,△ADM的面积最大?并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条公路环绕山脚的部分是一段圆弧形状(O为圆心),过A,B两点的切线交于点C,测得∠C=120°,A,B两点之间的距离为60m,则这段公路AB的长度是( )
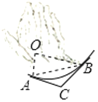
A.10πmB.20πmC.10![]() πmD.60m
πmD.60m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com