
【题目】为了鼓励送彩电下乡,国家决定对购买彩电的农户实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图①所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益Z(元)会相应降低且Z与x之间也大致满足如图②所示的一次函数关系。

(1)在政府未出台补贴措施前,该商场销售彩电的总收益额为多少元?
(2)在政府补贴政策实施后,分别求出该商场销售彩电台数y和每台家电的收益z与政府补贴款额x之间的函数关系式;
(3)要使该商场销售彩电的总收益w(元)最大,政府应将每台补贴款额x定为多少并求出总收益w的最大值。
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列各式中,计算正确的是( )
A. (a﹣b)2=a2﹣b2 B. (2x﹣y)2=4x2﹣2xy+y2
C. (a﹣3b)(a+3b)=a2﹣9b2 D. (15 x2 y-10x y2) ÷5xy=3x-2 y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动. 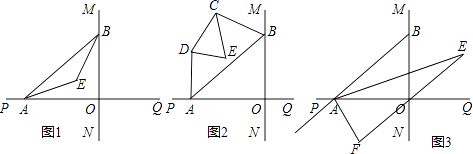
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A,B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A,B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E,F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.

(1)求证:AE=EF;
(2)如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,(1)中的结论是否仍然成立? ;(填“成立”或“不成立”);
(3)如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请证明,若不成立说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知二次函数图象的顶点坐标为C(1,0),直线![]() 与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴
与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴![]() 上.
上.
(1)、求![]() 的值及这个二次函数的关系式;
的值及这个二次函数的关系式;
(2)、P为线段AB上的一个动点(点P与A、B不重合),过P作![]() 轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为
轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为![]() ,点P的横坐标为
,点P的横坐标为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)、D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年春季,蔬菜种植场在15公顷的大棚地里分别种植了茄子和西红柿,总费用是26.5万元.其中,种植茄子和西红柿每公顷的费用和每公顷获利情况如表:
每公顷费用(万元) | 每公顷获利(万元) | |
茄子 | 1.7 | 2.4 |
西红柿 | 1.8 | 2.6 |
请解答下列问题:
(1)求出茄子和西红柿的种植面积各为多少公顷?
(2)种植场在这一季共获利多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com