
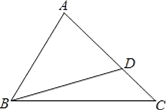
【题目】如图:△ABC中,∠C=45°,点D在AC上,且∠ADB=60°,AB为△BCD外接圆的切线.
(1)用尺规作出△BCD的外接圆(保留作图痕迹,可不写作法);
(2)求∠A的度数;
(3)求![]() 的值.
的值.
【答案】(1)作图见解析;(2)∠A=75°;(3)![]() =2.
=2.
【解析】试题分析:(1)利用三角形外接圆的圆心是各边垂直平分线的交点即可画出图形.
(2)只要证明△BOD是等腰直角三角形即可推出∠ABD=∠DBO=45°,利用三角形内角和定理即可解决问题.
(3)过点B作BE⊥AC,垂足为点E,设DE=x,则BD=2x,BE=![]() =
=![]() x,用x的代数式表示AD、DC即可解决问题.
x,用x的代数式表示AD、DC即可解决问题.
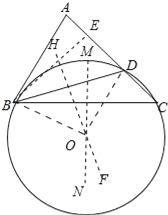
试题解析:(1)作BC的垂直平分线MN,作BD的垂直平分线HF,MN与FH的交点为O,以点O为圆心OB为作⊙O即可.如图所示:
;
(2)连结OB、OD,
由切线性质,知∠ABO=90°.
∵∠ACB=45°,∴∠BOD=90°(同弧所对的圆周角等于它所对的圆心角的一半).
∵OB=OD,∴∠OBD=∠ODB=45°,
由∠ABO=90°,得∠ABD=45°,∴∠A=180°﹣∠ABD﹣∠ADB=180°﹣45°﹣60°=75°;
(3)过点B作BE⊥AC,垂足为点E,
在Rt△BCE中,∵∠ACB=45°,∴∠EBC=45°,∴BE=CE.
在Rt△BDE中,∵∠DBE=90°﹣∠EDB=30°,∴BD=2DE,
设DE=x,则BD=2x,BE=![]() =
=![]() xDC=CE﹣DE=BE﹣DE=(
xDC=CE﹣DE=BE﹣DE=(![]() ﹣1)x.
﹣1)x.
AE=AD﹣DE=AD﹣x.
在△ABC和△ADB中,∵∠ABD=∠ACB=45°,∠A为公共角,∴△ABC∽△ADB,
∴![]() ,即AB2=ACAD,即
,即AB2=ACAD,即
AB2=(AD+DC)AD=AD2+AD(![]() ﹣1)x ①.
﹣1)x ①.
在Rt△ABE中,由勾股定理,得AB2=AE2+BE2=(AD﹣x)2+(![]() x)2 ②.
x)2 ②.
由①、②,得AD2+AD(![]() ﹣1)x=(AD﹣x)2+(
﹣1)x=(AD﹣x)2+(![]() x)2,
x)2,
化简整理,解得AD=2(![]() ﹣1)x.
﹣1)x.
∴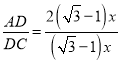 =2,
=2,
∴![]() =2.
=2.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2-3x+m=0的两实数根是( )
A. x1=1,x2=-1 B. x1=1,x2=2 C. x1=1,x2=0 D. x1=1,x2=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,义乌市民用汽车拥有量持续增长,2007年至2011年我市民用汽车拥有量依次约为:11,13,15,19,x(单位:万辆),这五个数的平均数为16,则x的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB∶OE=3∶2.其中正确结论的个数是( )
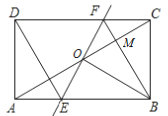
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
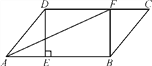
【题目】如图,在ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
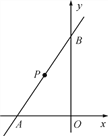
【题目】如图,在平面直角坐标系中,已知直线y=kx+6与x轴、y轴分别交于A,B两点,且△ABO的面积为12.
(1)求k的值;
(2)若点P为直线AB上的一动点,P点运动到什么位置时,△PAO是以OA为底的等腰三角形?求出此时点P的坐标;
(3)在(2)的条件下,连接PO,△PBO是等腰三角形吗?如果是,试说明理由;如果不是,请在线段AB上求一点C,使得△CBO是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的弦AB等于半径,连接OB并延长使BC=OB.
(1)∠ABC= .
(2)AC与⊙O有什么关系?请证明你的结论;
(3)在⊙O上,是否存在点D,使得AD=AC?若存在,请画出图形,并给出证明;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com