
【题目】在直角△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D,CE是△ABC的角平分线.
(1)求∠DCE的度数.
(2)若∠CEF=135°,求证:EF∥BC.

【答案】(1)15°(2)证明见解析
【解析】
(1)由图示知∠DCE=∠DCB-∠ECB,由∠B=30°,CD⊥AB于D,利用内角和定理,求出∠DCB的度数,又由角平分线定义得∠ECB=![]() ∠ACB,则∠DCE的度数可求;(2)根据∠CEF+∠ECB=180°,由同旁内角互补,两直线平行可以证明EF∥BC.
∠ACB,则∠DCE的度数可求;(2)根据∠CEF+∠ECB=180°,由同旁内角互补,两直线平行可以证明EF∥BC.
(1)∵∠B=30°,CD⊥AB于D,
∴∠DCB=90°-∠B=60°,
∵CE平分∠ACB,∠ACB=90°,
∴∠ECB=![]() ∠ACB=45°,
∠ACB=45°,
∴∠DCE=∠DCB-∠ECB=60°-45°=15°;
(2)∵∠CEF=135°,∠ECB=![]() ∠ACB=45°,
∠ACB=45°,
∴∠CEF+∠ECB=180°,
∴EF∥BC.


科目:初中数学 来源: 题型:
【题目】之前我们学习了一元一次方程的解法,下面是一道解一元一次方程的题:
解方程![]() ﹣
﹣![]() =1
=1
老师说:这是一道含有分母的一元一次方程,我们可以根据等式的性质,可以把方程的两边同乘以6,这样就可以去掉分母了.于是,小明按照老师说的方法进行了解答,小明同学的解题过程如下:
解:方程两边同时乘以6,得![]() ×6﹣
×6﹣![]() ×6=1…………①
×6=1…………①
去分母,得:2(2﹣3x)﹣3(x﹣5)=1………②
去括号,得:4﹣6x﹣3x+15=1……………③
移项,得:﹣6x﹣3x=1﹣4﹣15…………④
合并同类项,得﹣9x=﹣18……………⑤
系数化1,得:x=2………………⑥
上述小明的解题过程从第 步开始出现错误,错误的原因是 .
请帮小明改正错误,写出完整的解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
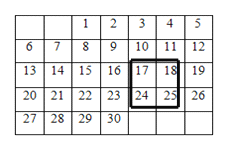
【题目】仔细观察下面的日历,回答下列问题:
(1)任意用正方形框圈出四个日期,如果正方形框中的第一个数(左上角的数)为![]() ,用代数式表示正方形框中的四个数的和;
,用代数式表示正方形框中的四个数的和;
(2)若将正方形框上下左右移动,可框住另外的四个数,这四个数的和能等于![]() 吗?如果能,依次写出这四个数;如果不能,请说明理由.
吗?如果能,依次写出这四个数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下表(注:水费按月份结算,![]() 表示立方米):请根据上表的内容解答下列问题:
表示立方米):请根据上表的内容解答下列问题:
(1)填空:若该户居民![]() 月份用水
月份用水![]() ,则应收水费___________元;
,则应收水费___________元;
(2)若该户居民![]() 月份用水
月份用水![]() (其中
(其中![]() ),则应收水费多少元?
),则应收水费多少元?
价目表
每月用水量 | 单价 |
不超过6 | 2元/ |
超出6 | 4元/ |
超出10 | 8元/ |
(3)若该户居民![]() 、
、![]() 两个月共用水
两个月共用水![]() (
(![]() 月份用水量超过了
月份用水量超过了![]() 月份),设
月份),设![]() 月份用水
月份用水![]() ,求该户居民
,求该户居民![]() 、
、![]() 两个月共交水费多少元?(答案可含有
两个月共交水费多少元?(答案可含有![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,D是BC边上的一个动点
是等边三角形,D是BC边上的一个动点![]() 点D不与B,C重合
点D不与B,C重合![]() 是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
![]() 如图1,求证:
如图1,求证:![]() ≌
≌![]() ;
;
![]() 请判断图1中四边形BCEF的形状,并说明理由;
请判断图1中四边形BCEF的形状,并说明理由;
![]() 若D点在BC边的延长线上,如图2,其它条件不变,请问
若D点在BC边的延长线上,如图2,其它条件不变,请问![]() 中结论还成立吗?如果成立,请说明理由.
中结论还成立吗?如果成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2 , 求原正方形空地的边长.设原正方形的空地的边长为xm,则可列方程为( ) 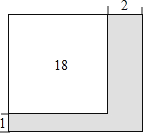
A.(x+1)(x+2)=18
B.x2﹣3x+16=0
C.(x﹣1)(x﹣2)=18
D.x2+3x+16=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=10,AC=2![]() ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.
【答案】10或6
【解析】试题解析:根据题意画出图形,如图所示,

如图1所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD+CD=8+2=10;
如图2所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD-CD=8-2=6,
则BC的长为6或10.
【题型】填空题
【结束】
12
【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种子商店销售“黄金一号”玉米种子,为惠民促销,推出两种销售方案供采购者选择.
方案一:每千克种子价格为4元,均不打折;
方案二:购买3千克以内(含3千克)的价格为每千克5元,若一次购买超过3千克,则超出部分的种子打七折.
(1)请分别求出方案一、方案二中购买的种子数量x(千克)与付款金额y(元)之间的函数关系式;
(2)若你去购买一定量的种子,你会怎样选择方案?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知∠DAB=∠DCB,AF平分∠DAB,CE平分∠DCB,∠FCE=∠CEB,试说明:AF∥CE。

解:(1)因为∠DAB=∠DCB( ),
又AF平分∠DAB,
所以_____=![]() ∠DAB( ),
∠DAB( ),
又因为CE平分∠DCB,
所以∠FCE=_____( ),
所以∠FAE=∠FCE。
因为∠FCE=∠CEB,
所以______=________
所以AF∥CE( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com