
 如图,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F,且AD交EF于O,则∠DOF的度数是90度.
如图,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F,且AD交EF于O,则∠DOF的度数是90度. 科目:初中数学 来源: 题型:选择题
 如图,折线ABCDE描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系.根据图中提供的信息,给出下列说法,其中正确的说法是( )
如图,折线ABCDE描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系.根据图中提供的信息,给出下列说法,其中正确的说法是( )| A. | 汽车共行驶了120千米 | |
| B. | 汽车自出发后前3小时的平均行驶速度为40千米/时 | |
| C. | 汽车在整个行驶过程中的平均速度为40千米/时 | |
| D. | 汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在菱形ABCD中,AB=10,AC=16,点M是对角线AC上的一个动点,过点M作PQ⊥AC交AB于点P,交AD于点Q,将△APQ沿PQ折叠,点A落在点E处,当△BCE是等腰三角形时,AP的长为$\frac{15}{4}$或$\frac{195}{4}$.
如图,在菱形ABCD中,AB=10,AC=16,点M是对角线AC上的一个动点,过点M作PQ⊥AC交AB于点P,交AD于点Q,将△APQ沿PQ折叠,点A落在点E处,当△BCE是等腰三角形时,AP的长为$\frac{15}{4}$或$\frac{195}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
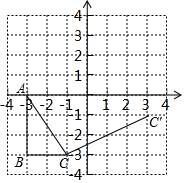 如图,在平面直角坐标系中,Rt△ABC的三个顶点坐标为A(-3,0),B(-3,-3),C(-1,-3)
如图,在平面直角坐标系中,Rt△ABC的三个顶点坐标为A(-3,0),B(-3,-3),C(-1,-3)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查江北中小学的睡眠时间 | |
| B. | 调查重庆市初中生的兴趣爱好 | |
| C. | 调查中国中学教师的健康状况 | |
| D. | 调查“天宫二号”飞行器各零部件质量 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com