
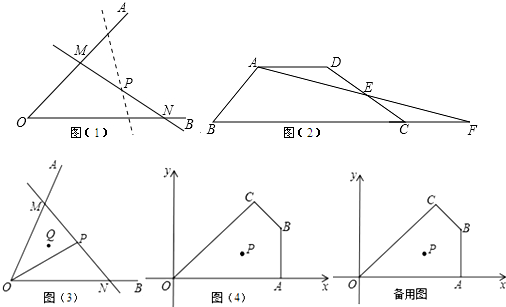
分析 (1)根据问题情境的结论可以得出当直线旋转到点P是MN的中点时S△MON最小,过点M作MG∥OB交EF于G.由全等三角形的性质可以得出结论;
实际运用:如图3,作PP1⊥OB,MM1⊥OB,垂足分别为P1,M1,再根据条件由三角函数值就可以求出结论;
(2)分情况讨论当过点P的直线l与四边形OABC的一组对边OC、AB分别交于点M、N,延长OC、AB交于点D,由条件可以得出AD=6,就可以求出△OAD的面积,再根据问题迁移的结论就可以求出最大值;
(3)当过点P的直线l与四边形OABC的另一组对边CB、OA分别交M、N,延长CB交x轴于T,由B、C的坐标可得直线BC的解析式,就可以求出T的坐标,从而求出△OCT的面积,再由问题迁移的结论可以求出最大值,通过比较就可以求出结论.
解答 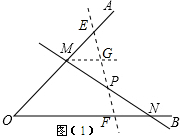 解:(1)当直线旋转到点P是MN的中点时S△MON最小,
解:(1)当直线旋转到点P是MN的中点时S△MON最小,
如图(1),过点P的另一条直线EF交OA、OB于点E、F,设PF<PE,过点M作MG∥OB交EF于G,
由方法探究可以得出当P是MN的中点时S四边形MOFG=S△MON.
∵S四边形MOFG<S△EOF,
∴S△MON<S△EOF,
∴当点P是MN的中点时S△MON最小;
(2)实际运用:如图3,作PP1⊥OB,MM1⊥OB,垂足分别为P1,M1,
在Rt△OPP1中,∠POB=30°,
∴PP1=$\frac{1}{2}$OP=2km,OP1=OP cos∠POB=2$\sqrt{3}$km,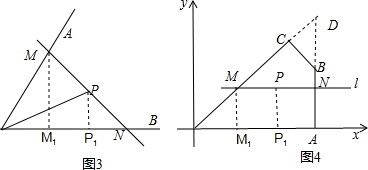
由方法探究的结论知道,当PM=PN时,△MON的面积最小,
∵PP1∥MM1
∴△N PP1∽△NMM1
∴MM1=2PP1=4 km,M1P1=P1N,
在Rt△OMM1中,∠AOB=70°,
∴OM1=$\frac{{MM}_{1}}{tan∠AOB}$=$\frac{4}{tan70°}$ km,
∴M1P1=P1N=(2$\sqrt{3}$-$\frac{4}{tan70°}$) km,
∴ON=OP1+P1N=2$\sqrt{3}$+(2$\sqrt{3}$-$\frac{4}{tan70°}$)=(4$\sqrt{3}$-$\frac{4}{tan70°}$) km,
∴S△MON=$\frac{1}{2}$ON•MM1=$\frac{1}{2}$ (4$\sqrt{3}$-$\frac{4}{tan70°}$)×4≈10.8km.
(3)拓展延伸:①如图4,当过点P的直线l与四边形OABC的一组对边OC、AB分别交于点M、N,延长OC、AB交于点D,
∵C($\frac{9}{2}$,$\frac{9}{2}$),
∴∠AOC=45°,
∴AO=AD.
∵A(6,0),
∴OA=6,
∴AD=6.
∴S△AOD=$\frac{1}{2}$×6×6=18,
由问题迁移的结论可知,当PN=PM时,△MND的面积最小,
∴四边形ANMO的面积最大.
作PP1⊥OA,MM1⊥OA,垂足分别为P1,M1,
∴M1P1=P1A=2,
∴OM1=M1M=2,
∴MN∥OA,
∴S四边形OANM=S△OMM1+S四边形ANMM1=$\frac{1}{2}$×2×2+2×4=10
②如图5,当过点P的直线l与四边形OABC的另一组对边CB、OA分别交M、N,延长CB交x轴于T,
∵C($\frac{9}{2}$,$\frac{9}{2}$)、B(6,3),设直线BC的解析式为y=kx+b,由题意,得
$\left\{\begin{array}{l}{\frac{9}{2}=\frac{9}{2}k+b}\\{3=6k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=9}\end{array}\right.$,
∴y=-x+9,
当y=0时,x=9,
∴T(9,0).
∴S△OCT=$\frac{1}{2}$×$\frac{9}{2}$×$9=\frac{81}{4}$,
由问题迁移的结论可知,当PM=PN时,△MNT的面积最小,
∴四边形CMNO的面积最大.
∴NP1=M1P1,MM1=2PP1=4,
∴4=-x+9,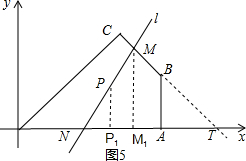
∴x=5,
∴M(5,4),
∴OM1=5,
∵P(4,2),
∴OP1=4,
∴P1M1=NP1=1,
∴ON=3,
∴NT=6,
∴S△MNT=$\frac{1}{2}$×4×6=12,
∴S四边形OCMN=$\frac{81}{4}$-12=$\frac{33}{4}$<10.
∴综上所述:截得四边形面积的最大值为10.
点评 本题考查了由特殊到一般的数学思想的运用,全等三角形的判定及性质的运用,勾股定理的运用,待定系数法求一次函数的解析式的运用,四边形的面积公式的运用,三角形的面积公式的运用,分类讨论思想的运用,解答时建立数学模型解答是关键.


科目:初中数学 来源: 题型:解答题
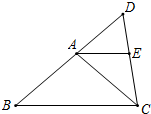 如图,在△ABC中,AB=AC=5cm,∠DCA=∠B,点D在BA延长线上,AE∥BC,交CD于点E,AE=$\frac{25}{8}$cm.
如图,在△ABC中,AB=AC=5cm,∠DCA=∠B,点D在BA延长线上,AE∥BC,交CD于点E,AE=$\frac{25}{8}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2006 | B. | 1-20072 | C. | 1-20062 | D. | 123456 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,5),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动(即:沿着长方形移动一周)
如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,5),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动(即:沿着长方形移动一周)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com