
【题目】如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
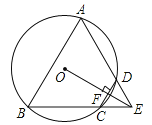
(1)求证:∠A=∠AEB;
(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.
【答案】(1)证明见试题解析;(2)证明见试题解析.
【解析】
试题(1)根据圆内接四边形的性质可得∠A+∠BCD=180°,由邻补角互补可得∠DCE+∠BCD=180°,进而得到∠A=∠DCE,然后利用等边对等角可得∠DCE=∠AEB,进而可得∠A=∠AEB;
(2)先证明△DCE是等边三角形,进而可得∠AEB=60°,再根据∠A=∠AEB,可得△ABE是等腰三角形,进而可得△ABE是等边三角形.
试题解析:(1)∵四边形ABCD是⊙O的内接四边形,∴∠A+∠BCD=180°,∵∠DCE+∠BCD=180°,∴∠A=∠DCE,∵DC=DE,∴∠DCE=∠AEB,∴∠A=∠AEB;
(2)∵∠A=∠AEB,∴△ABE是等腰三角形,∵EO⊥CD,∴CF=DF,∴EO是CD的垂直平分线,∴ED=EC,∵DC=DE,∴DC=DE=EC,∴△DCE是等边三角形,∴∠AEB=60°,∴△ABE是等边三角形.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AB=DC,点M,N分别是AD,BC的中点,点E,F分别是BM,CM的中点. (1)求证:四边形MENF是菱形; (2)当四边形MENF是正方形时,求证:等腰梯形ABCD的高是底边BC的一半.
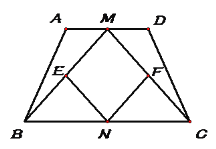
查看答案和解析>>
科目:初中数学 来源: 题型:
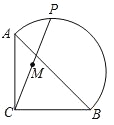
【题目】如图,在等腰 Rt△ABC 中,AC=BC= 2![]() ,点 P 在以斜边 AB 为直径的半圆上,M 为 PC的中点.当点 P 沿半圆从点 A 运动至点 B 时,点 M 运动的路径长是( )
,点 P 在以斜边 AB 为直径的半圆上,M 为 PC的中点.当点 P 沿半圆从点 A 运动至点 B 时,点 M 运动的路径长是( )
A. 2 B. 2 ![]() C. π D.
C. π D. ![]() π
π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系式和自变量![]() 的取值范围;
的取值范围;
(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用勾股定理得到结论:P1P2=![]() ;他还证明了线段P1P2的中点P(x,y)的坐标公式是:x=
;他还证明了线段P1P2的中点P(x,y)的坐标公式是:x=![]() ,y=
,y=![]() ;
;
启发应用
请利用上面的信息,解答下面的问题:
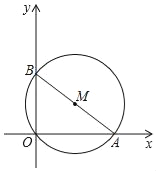
如图,在平面直角坐标系中,已知A(8,0),B(0,6),C(1,7),⊙M经过原点O及点A、B.
(1)求⊙M的半径及圆心M的坐标;
(2)判断点C与⊙M的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
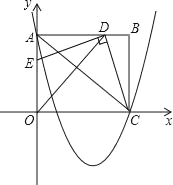
【题目】如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,C在x轴的正半轴上,已知A(0,8)、C(10,0),作∠AOC的平分线交AB于点D,连接CD,过点D作DE⊥CD交OA于点E.
(1)求点D的坐标;
(2)求证:△ADE≌△BCD;
(3)抛物线y=![]() x2﹣
x2﹣![]() x+8经过点A、C,连接AC.探索:若点P是x轴下方抛物线上一动点,过点P作平行于y轴的直线交AC于点M.是否存在点P,使线段MP的长度有最大值?若存在,求出点P的坐标;若不存在,请说明理由.
x+8经过点A、C,连接AC.探索:若点P是x轴下方抛物线上一动点,过点P作平行于y轴的直线交AC于点M.是否存在点P,使线段MP的长度有最大值?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图1:
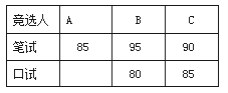
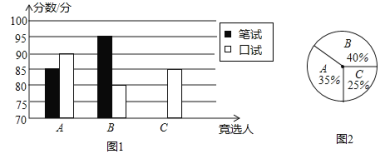
(1)请将表和图1中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图2(没有弃权票,每名学生只能推荐一个),则B在扇形统计图中所占的圆心角的度数是______.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c 如图所示,直线x=-1是其对称轴,

(1)确定a,b,c, Δ=b2-4ac的符号,
(2)求证:a-b+c>0,
(3)当x取何值时,y>0;当x取何值时y<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com