
 ,点D在AB边上(点D与点A,B不重合),DE∥BC交AC边于点E,点F在线段EC上,且EF=
,点D在AB边上(点D与点A,B不重合),DE∥BC交AC边于点E,点F在线段EC上,且EF= AE,以DE、EF为邻边作平行四边形DEFG,连接BG.
AE,以DE、EF为邻边作平行四边形DEFG,连接BG.
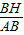 =
= 可得出AH、BC的长,进而可得出△ABC的面积,由相似三角形的判定定理得出△ADE∽△ABC,根据相似三角形面积的比等于相似比即可得出△ADE的面积;
可得出AH、BC的长,进而可得出△ABC的面积,由相似三角形的判定定理得出△ADE∽△ABC,根据相似三角形面积的比等于相似比即可得出△ADE的面积;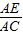 =
=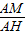 =
=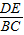 ,再根据AE=x,可知AM=
,再根据AE=x,可知AM= x,DE=
x,DE= x,NH=8-x,根据S△DBG=S梯形DBCE-S平行四边形DGFE-S梯形GBCF,即可得出结论;
x,NH=8-x,根据S△DBG=S梯形DBCE-S平行四边形DGFE-S梯形GBCF,即可得出结论; x,cosC=cos∠ABC=
x,cosC=cos∠ABC= ,可知PC=6-
,可知PC=6- x,BQ=12-
x,BQ=12- x-(6-
x-(6- x)=6-
x)=6-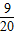 x,由勾股定理可用x表示出BG的长,在△DBG中用x表示出DB,DG的长,再分DB=DG和DB=BG两种情况进行讨论.
x,由勾股定理可用x表示出BG的长,在△DBG中用x表示出DB,DG的长,再分DB=DG和DB=BG两种情况进行讨论.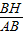 =
= ,AB=10,
,AB=10, ×12×8=48.
×12×8=48.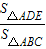 =(
=(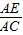 )2,
)2, AE,EF=FC,
AE,EF=FC,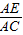 =
= =
= ,
,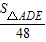 =
= ,
,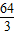 ;
;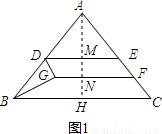 (2)设AH交DE、GF于点M、N.
(2)设AH交DE、GF于点M、N. =
=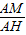 =
=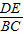 ,
, x,DE=
x,DE= x,
x, AM=
AM= x,∴NH=8-x,
x,∴NH=8-x, (
( x+12)(8-
x+12)(8- x)-
x)- x•
x• x-
x- (
( x+12)(8-x),
x+12)(8-x),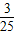 x2+
x2+ x(0<x≤8);
x(0<x≤8); x,cosC=cos∠ABC=
x,cosC=cos∠ABC= ,
, x,
x,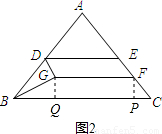
 x-(6-
x-(6- x)=6-
x)=6-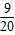 x,
x,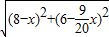 ,
, x,
x, x,解得x=8;
x,解得x=8;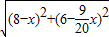 ,
,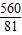 ,
,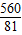 .
.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为A、
| ||||
B、(
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com