
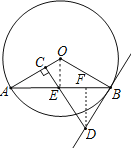
【题目】如图,AB是⊙O的弦,过AB的中点E作EC⊥OA,垂足为C,过点B作直线BD交CE的延长线于点D,使得DB=DE.
(1)求证:BD是⊙O的切线;
(2)若AB=12,DB=5,求△AOB的面积.

【答案】(1)证明见解析;(2)27.
【解析】(1)根据等腰三角形的性质和切线的判定方法可以求得∠OBD的度数,从而可以证明结论成立;
(2)要求△AOB的面积只要求出OE的长即可,根据题目中的条件和三角形相似的知识可以求得OE的长,从而可以解答本题.
(1)∵OA=OB,DB=DE,
∴∠A=∠OBA,∠DEB=∠DBE,
∵EC⊥OA,∠DEB=∠AEC,
∴∠A+∠DEB=90°,
∴∠OBA+∠DBE=90°,
∴∠OBD=90°,
∵OB是圆的半径,
∴BD是⊙O的切线;
(2)过点D作DF⊥AB于点F,连接OE,
∵点E是AB的中点,AB=12,
∴AE=EB=6,OE⊥AB,
又∵DE=DB,DF⊥BE,DB=5,DB=DE,
∴EF=BF=3,
∴DF=![]() =4,
=4,
∵∠AEC=∠DEF,
∴∠A=∠EDF,
∵OE⊥AB,DF⊥AB,
∴∠AEO=∠DFE=90°,
∴△AEO∽△DFE,
∴![]() ,
,
即![]() ,得EO=4.5,
,得EO=4.5,
∴△AOB的面积是:![]() =27.
=27.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=∠ACB,点D、E分别是AC、AB上两点,且AD=AE.CE、BD交于点O.
⑴ 求证:OB=OC;
⑵ 连接ED,若ED=EB,试说明BD平分∠ABC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,M是AB边上的中点,点D、E分别是AC、BC边上的动点,连接DM 、ME、CM、DE, DE与CM相交于点F且∠DME=90°.则下列5个结论: (1)图中共有两对全等三角形;(2)△DEM是等腰三角形; (3)∠CDM=∠CFE;(4)AD2+BE2=DE2;(5)四边形CDME的面积发生改变.其中正确的结论有( )个.

A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:
 =
= =
=![]() =
=![]() -2;
-2;
 =
= =
=![]() .
.
请回答下列问题:
(1)观察上面的解题过程,请直接写出式子![]() = ;
= ;
(2)观察上面的解题过程,请直接写出式子![]() = ;
= ;
(3)利用上面所提供的解法,请求![]() +···+
+···+![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABOC是正方形,点A的坐标为(1,1),![]() 是以点B为圆心,BA为半径的圆弧;
是以点B为圆心,BA为半径的圆弧;![]() 是以点O为圆心,OA1为半径的圆弧,
是以点O为圆心,OA1为半径的圆弧,![]() 是以点C为圆心,CA2为半径的圆弧,
是以点C为圆心,CA2为半径的圆弧,![]() 是以点A为圆心,AA3为半径的圆弧,继续以点B、O、C、A为圆心按上述作法得到的曲线AA1A2A3A4A5…称为正方形的“渐开线”,那么点A5的坐标是______,点A2018的坐标是______.
是以点A为圆心,AA3为半径的圆弧,继续以点B、O、C、A为圆心按上述作法得到的曲线AA1A2A3A4A5…称为正方形的“渐开线”,那么点A5的坐标是______,点A2018的坐标是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)求证:EG=CG且EG⊥CG;
(2)将图①中△BEF绕B点逆时针旋转45,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
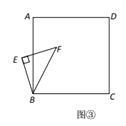
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,∠ACB=900,且A(0,4),点C(2,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D。
(1)求证;△AOC≌△CEB
(2)求△ABD的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知 三角形ABC各顶点在格点上
(1)直接写出三角形ABC的三个顶点的坐标
A B C ;
(2)画出三角形ABC关于y轴对称的三角形A′B′C′.
(3)求三角形ABC的面积;
(4)直接与出A′C′与y轴交点的坐标 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com