
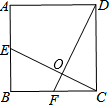
 如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连接CE、DF,CE与DF交于点O,求证:
如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连接CE、DF,CE与DF交于点O,求证:分析 (1)根据SAS证明△BEC≌△CFD,得EC=DF;
(2)由全等得:∠FDC=∠BCE,因为∠DFC+∠FDC=90°,等量代换可得结论.
解答 证明:(1)∵四边形ABCD为正方形,
∴AB=BC=DC,∠ABC=∠FCD=90°,
∵E是边AB的中点,F是边BC的中点,
∴BE=$\frac{1}{2}$AB,FC=$\frac{1}{2}$BC,
∴BE=FC,
在△BEC和△CFD中,
∵$\left\{\begin{array}{l}{BE=FC}\\{∠ABC=∠FCD}\\{BC=CD}\end{array}\right.$,
∴△BEC≌△CFD(SAS),
∴EC=DF;
(2)由(1)得:△BEC≌△CFD,
∴∠FDC=∠BCE,
∵∠FCD=90°,
∴∠DFC+∠FDC=90°,
∴∠DFC+∠BCE=90°,
∴∠FOC=90°,
∴CE⊥DF.
点评 本题考查了正方形的性质和全等三角形的性质和判定,属于常考题型,准确证明EC和DF所在的直角三角形全等是本题的关键,同时要熟练掌握正方形的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中模拟数学试卷(解析版) 题型:解答题
何老师安排喜欢探究问题的小明解决某个问题前,先让小明看了一个有解答过程的例题.
例:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
【解析】
∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0∴m=﹣3,n=3
为什么要对2n2进行了拆项呢?
聪明的小明理解了例题解决问题的方法,很快解决了下面两个问题.相信你也能很好的解决下面的这两个问题,请写出你的解题过程..
解决问题:
(1)若x2﹣4xy+5y2+2y+1=0,求xy的值;
(2)已知a、b、c是△ABC的三边长,满足a2+b2=10a+12b﹣61,c是△ABC中最短边的边长,且c为整数,那么c可能是哪几个数?
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中模拟数学试卷(解析版) 题型:单选题
某工厂现有95个工人,一个工人每天可做8个螺杆或22个螺母,两个螺母和一个螺杆为一套,现在要求工人每天做的螺杆和螺母完整配套而没有剩余,若设安排x个工人做螺杆,y个工人做螺母,则列出正确的二元一次方程组为( )
A. 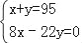 ; B.
; B. 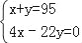 ; C.
; C. 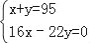 ; D.
; D. 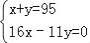
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com