
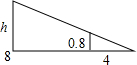
 如图,小伟在打网球时,击球点距离球网的水平距离是8米.已知网高是0.8米,要使球恰好能打过网,且落在离网4米的位置,则球拍击打的高度h为( )
如图,小伟在打网球时,击球点距离球网的水平距离是8米.已知网高是0.8米,要使球恰好能打过网,且落在离网4米的位置,则球拍击打的高度h为( )| A. | 1.0 | B. | 1.6 | C. | 2.0 | D. | 2.4 |
分析 如图,BD=8m,AD=4m,DE=0.8m,证明△ADE∽△ABC,利用相似比得到$\frac{0.8}{h}$=$\frac{4}{4+8}$,然后利用比例性质求h即可.
解答 解:如图,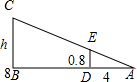 BD=8m,AD=4m,DE=0.8m,
BD=8m,AD=4m,DE=0.8m,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}$=$\frac{AD}{AB}$,即$\frac{0.8}{h}$=$\frac{4}{4+8}$,
∴h=2.4(m).
故选D.
点评 本题考查了相似三角形的应用:利用杆或直尺测量物体的高度就是利用杆或直尺的高(长)作为三角形的边,利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.


科目:初中数学 来源: 题型:填空题
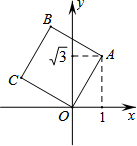 如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,$\sqrt{3}$),则(1)OA的长为2,(2)点C的坐标为(-$\sqrt{3}$,1).
如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,$\sqrt{3}$),则(1)OA的长为2,(2)点C的坐标为(-$\sqrt{3}$,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
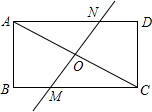 如图,将矩形ABCD沿直线MN对折,使A、C重合,直线MN交AC于O,且AB=6,BC=8
如图,将矩形ABCD沿直线MN对折,使A、C重合,直线MN交AC于O,且AB=6,BC=8查看答案和解析>>
科目:初中数学 来源: 题型:填空题
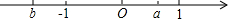 实数a、b在数轴上的位置如图所示,写出不等式组$\left\{\begin{array}{l}x+a>0\\ x-b>0\end{array}$的解集为x>-a.
实数a、b在数轴上的位置如图所示,写出不等式组$\left\{\begin{array}{l}x+a>0\\ x-b>0\end{array}$的解集为x>-a.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
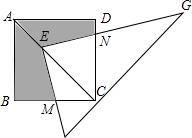 如图,点E在正方形ABCD的对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为2,图中阴影部分的面积为( )
如图,点E在正方形ABCD的对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为2,图中阴影部分的面积为( )| A. | 2 | B. | $\frac{4}{3}$ | C. | $\frac{16}{9}$ | D. | $\frac{20}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
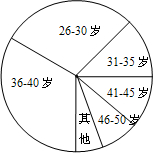 2012年3月全国两会在北京召开,公众最关心哪些问题?九一班学生就老百姓最关注的两会热点问题,在网络上发布了相应的调查问卷,到目前为止,共有不同年龄段的2880人参与,其中31~35岁关心问题的具体情况统计如下:
2012年3月全国两会在北京召开,公众最关心哪些问题?九一班学生就老百姓最关注的两会热点问题,在网络上发布了相应的调查问卷,到目前为止,共有不同年龄段的2880人参与,其中31~35岁关心问题的具体情况统计如下:| 关心问题 | 频数 | 频率 |
| 收入分配 | 90 | 0.25 |
| 住房问题 | 54 | 0.15 |
| 物价调控 | 36 | 0.1 |
| 医疗改革 | 18 | 0.05 |
| 养老保险 | 54 | 0.15 |
| 其他 | 108 | 0.30 |
| 合计 | 360 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
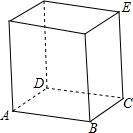 如图是一个长方体,AB=x,BC=$\frac{6}{5}$x,CE=10,则长方体的体积y与x之间的函数解析式是y=12x2,y是x的二次函数.
如图是一个长方体,AB=x,BC=$\frac{6}{5}$x,CE=10,则长方体的体积y与x之间的函数解析式是y=12x2,y是x的二次函数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com