

 =6-3
=6-3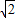 ,则点P的坐标是(12-6
,则点P的坐标是(12-6 ,0);
,0); =
= (6+2x),x=3
(6+2x),x=3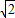 ,则P点的坐标是(-6
,则P点的坐标是(-6 ,0).
,0).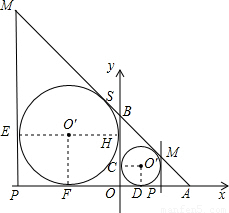 解:①如图,当⊙O′在y轴的右侧时,MP在圆的左侧,
解:①如图,当⊙O′在y轴的右侧时,MP在圆的左侧,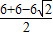 =6-3
=6-3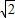 ,
,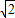 ,0);
,0); ,
,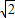 =
= (6+2x),
(6+2x),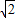 ,
,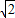 ,0).
,0).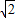 ,0),(12-6
,0),(12-6 ,0).
,0).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2002年全国中考数学试题汇编《圆》(07)(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《圆》(01)(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2002年山东省济南市中考数学试卷(解析版) 题型:填空题
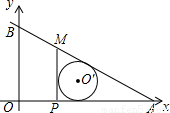
查看答案和解析>>
科目:初中数学 来源:2002年山东省济南市中考数学试卷(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:2002年山东省济南市中考数学试卷(解析版) 题型:选择题
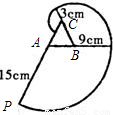
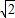 的正方形ABCD厚纸板,按照下面做法,做了一套七巧板:作图①,作对角线AC,分别取AB,BC中点E,F,连接EF作DG⊥EF于G,交AC于H,过G作GL∥BC,交AC于L,再由E作EK∥DG,交AC于K,将正方形ABCD沿画出的线剪开,现由它拼出一座桥(如图②),这座桥的阴影部分的面积是( )
的正方形ABCD厚纸板,按照下面做法,做了一套七巧板:作图①,作对角线AC,分别取AB,BC中点E,F,连接EF作DG⊥EF于G,交AC于H,过G作GL∥BC,交AC于L,再由E作EK∥DG,交AC于K,将正方形ABCD沿画出的线剪开,现由它拼出一座桥(如图②),这座桥的阴影部分的面积是( )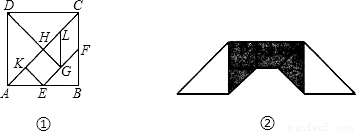
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com