
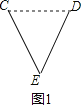
【题目】如图1所示的晾衣架,支架主视图的基本图形是菱形,其示意图如图2,晾衣架伸缩时,点G在射线DP上滑动,∠CED的大小也随之发生变化,已知每个菱形边长均等于20cm,且AH=DE=EG=20cm.

(1)当∠CED=60°时,CD=________cm.
(2)当∠CED由60°变为120°时,点A向左移动了________cm(结果精确到0.1cm)(参考数据 ![]() ≈1.73).
≈1.73).
【答案】 20 43.9
【解析】试题分析:(1)证明△CED是等边三角形,即可求解;
(2)分别求得当∠CED是60°和120°,两种情况下AD的长,求差即可.
试题解析:(1)连接CD(图1),
∵CE=DE,∠CED=60°,
∴△CED是等边三角形,
∴CD=DE=20cm;
(2)根据题意得:AB=BC=CD,
当∠CED=60°时,AD=3CD=60cm,
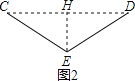
当∠CED=120°时,过点E作EH⊥CD于H(图2),则∠CEH=60°,CH=HD,
在直角△CHE中,sin∠CEH=![]() ,
,
∴CH=20sin60°=20×![]() =10
=10![]() (cm),
(cm),
∴CD=20![]() cm,
cm,
∴AD=3×20![]() =60
=60![]() ≈103.9(cm),
≈103.9(cm),
∴103.9-60=43.9(cm),
即点A向左移动了43.9cm.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌![]() ,△AEB≌
,△AEB≌![]() ,且
,且![]() ,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )

A.105°B.100°C.110°D.115°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂接到订单,需要边长为(a+3)和3的两种正方形卡纸.
(1)仓库只有边长为(a+3)的正方形卡纸,现决定将部分边长为(a+3)的正方形纸片,按图甲所示裁剪得边长为3的正方形.

①如图乙,求裁剪正方形后剩余部分的面积(用含a代数式来表示);
②剩余部分沿虚线又剪拼成一个如图丙所示长方形(不重叠无缝隙),则拼成的长方形的边长多少?(用含a代数式来表示);
(2)若将裁得正方形与原有正方形卡纸放入长方体盒子底部,按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),盒子底部中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2测得盒子底部长方形长比宽多3,则S2﹣S1的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
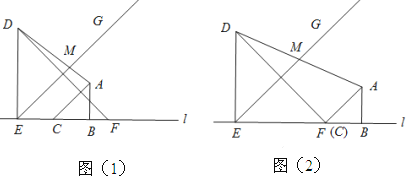
【题目】如图1,两个等腰直角三角板![]() 和
和![]() 有一条边在同一条直线
有一条边在同一条直线![]() 上,
上, ![]() ,
, ![]() .将射线
.将射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,交直线
,交直线![]() 于点
于点![]() .将图1中的三角板
.将图1中的三角板![]() 沿直线
沿直线![]() 向右平移,设
向右平移,设![]() 、
、![]() 两点间的距离为
两点间的距离为![]() .
.
解答问题:
(1)①当点![]() 与点
与点![]() 重合时,如图2所示,可得
重合时,如图2所示,可得![]() 的值为 ;
的值为 ;
②在平移过程中, ![]() 的值为 (用含
的值为 (用含![]() 的代数式表示);
的代数式表示);
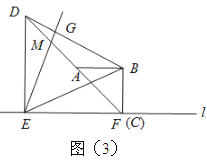
(2)将图2中的三角板![]() 绕点
绕点![]() 逆时针旋转,原题中的其他条件保持不变.当点
逆时针旋转,原题中的其他条件保持不变.当点![]() 落在线段
落在线段![]() 上时,如图3所示,计算
上时,如图3所示,计算![]() 的值;
的值;
(3)将图1中的三角板ABC绕点C逆时针旋转![]() 度,
度, ![]() ≤
≤![]() ,原题中的其他条件保持不变.如图4所示,请补全图形,计算
,原题中的其他条件保持不变.如图4所示,请补全图形,计算![]() 的值(用含k的代数式表示).
的值(用含k的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 运动;同时动点
运动;同时动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 运动,运动时间是
运动,运动时间是![]() 秒.
秒.

(1)用含![]() 的代数式表示
的代数式表示![]() 的长度.
的长度.
(2)在运动过程中,是否存在某一时刻![]() ,使点
,使点![]() 位于线段
位于线段![]() 的垂直平分线上?若存在,求出
的垂直平分线上?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)是否存在某一时刻![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(4)是否存在某一时刻![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定:
坡度 | 1:20 | 1:16 | 1:12 |
最大高度(米) | 1.50 | 1.00 | 0.75 |
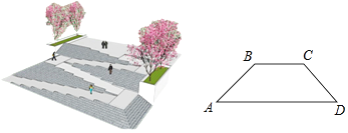
(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一款口罩,每袋的进价为12元,计划售价大于12元但不超过22元,通过试场调查发现,这种口罩每袋售价提高1元,日均销售量降低5袋,当售价为18元时,日均销售量为50袋.
(1)在售价为18元的基础上,将这种口罩的售价每袋提高x元,则日均销售量是 袋;(用含x的代数式表示)
(2)要想销售这种口罩每天赢利275元,该商场每袋口罩的售价要定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB⊥BC,对角线AC、BD相交于点E,E为BD中点,且AD=BD,AB=2,∠BAC=30°,则DC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张长方形纸板按图中虚线裁剪成![]() 块,其中有
块,其中有![]() 块是边长都为
块是边长都为![]() 厘米的大正方形,
厘米的大正方形,![]() 块是边长都为
块是边长都为![]() 厘米的小正方形,
厘米的小正方形,![]() 块是长为
块是长为![]() 厘米,宽为
厘米,宽为![]() 厘米的一模一样的小长方形,且
厘米的一模一样的小长方形,且![]() ,设图中所有裁剪线(虚线部分)长之和为
,设图中所有裁剪线(虚线部分)长之和为![]() 厘米.
厘米.

(1)![]() ______(试用
______(试用![]() ,
,![]() 的代数式表示);
的代数式表示);
(2)若每块小长方形的面积为![]() 平方厘米,四个正方形的面积和为
平方厘米,四个正方形的面积和为![]() 平方厘米,求
平方厘米,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com