
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是一个大于
是一个大于![]() 而小于
而小于![]() 的整数,且方程的两个根都是有理数,求
的整数,且方程的两个根都是有理数,求![]() 的值和它的两个根;
的值和它的两个根;
(2)若方程![]() 有两个不相等的实数根,试判断另一个关于
有两个不相等的实数根,试判断另一个关于![]() 的方程
的方程![]() 的根的情况.
的根的情况.
【答案】![]() 的值为
的值为![]() 和它的另一个根为
和它的另一个根为![]() 或
或![]() ;
;![]() 此方程有两个不相等的实数根.
此方程有两个不相等的实数根.
【解析】
(1)根据题意结合方程有两个有理根得出m=9,进而求出即可;
(2)利用根的判别式得出m的取值范围,进而得出答案.
(1)∵x2﹣2x+1=m,∴(x﹣1)2=m.
∵m是一个大于5而小于10的整数,且方程的两个根都是有理数,∴m=9,∴x﹣1=±3,解得:x1=4,x2=﹣2,故m的值为9和它的另一个根为-2或4;
(2)∵方程x2﹣2x﹣m+1=0有两个不相等的实数根,∴△=b2﹣4ac=4﹣4(1﹣m)>0,即m>0.
∵另一个关于x的方程x2﹣(m﹣2)x+1﹣2m=0,△=b2﹣4ac=(m﹣2)2﹣4(1﹣2m)=m2+4m=m(m+4).
又∵m>0,∴m+4>0,∴△=b2﹣4ac=m(m+4)>0,∴此方程有两个不相等的实数根.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元![]() 已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
![]() 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价;
![]() 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变![]() 要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当你站在博物馆的展览厅中时,你知道站在何处观赏最理想吗?如图,设墙壁上的展品最高点P距地面2.5米,最低点Q距地面2米,观赏者的眼睛F距地面1.6米,当视角∠PEQ最大时,站在此处观赏最理想,则此时E到墙壁的距离为( )米.

A. 1 B. 0.6 C. 0.5 D. 0.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,长方形OABC的顶点A,B的坐标分别为A(6,0),B(6,4),D是BC的中点,动点P从O点出发,以每秒1个单位长度的速度,沿着O→A→B→D运动,设点P运动的时间为t秒(0<t<13).
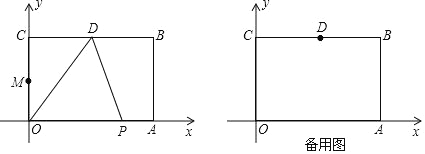
(1)①点D的坐标是(___,___);
②当点P在AB上运动时,点P的坐标是(___,___)(用t表示);
(2)写出△POD的面积S与t之间的函数关系式,并求出△POD的面积等于9时点P的坐标;
(3)当点P在OA上运动时,连接BP,将线段BP绕点P逆时针旋转,点B恰好落到OC的中点M处,则此时点P运动的时间t=___秒.(直接写出参考答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(1,0),B(2,﹣3),C(4,﹣2).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1向左平移3个单位长度后得到的△A2B2C2;
(3)如果AC上有一点P(m,n)经过上述两次变换,那么对应A2C2上的点P2的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆客房部有![]() 个房间供游客居住,当每个房间的定价为每天
个房间供游客居住,当每个房间的定价为每天![]() 元时,所有房间刚好可以住满,根据经验发现,每个房间的定价每增加
元时,所有房间刚好可以住满,根据经验发现,每个房间的定价每增加![]() 元,就会有
元,就会有![]() 个房间空闲,对有游客入住的房间,宾馆需对每个房间支出每天
个房间空闲,对有游客入住的房间,宾馆需对每个房间支出每天![]() 元的各种费用.设每个房间的定价增加
元的各种费用.设每个房间的定价增加![]() 元,每天的入住量为
元,每天的入住量为![]() 个,客房部每天的利润为
个,客房部每天的利润为![]() 元.
元.
![]() 求
求![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 求
求![]() 与
与![]() 的函数关系式,并求客房部每天的最大利润是多少?
的函数关系式,并求客房部每天的最大利润是多少?
![]() 当
当![]() 为何值时,客房部每天的利润不低于
为何值时,客房部每天的利润不低于![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①两条对角线相等的四边形是矩形;②有一组对边相等,一组对角是直角的四边形是矩形;③有一个角为直角,两条对角线相等的四边形是矩形;④四个角都相等的四边形是矩形⑤相邻两边都互相垂直的四边形是矩形.其中判断正确的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com