
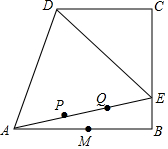
 如图四边形ABCD,∠B=∠C=90°,AB=BC=4,△AED为等边三角形,M为AB中点,E为BC上一点,动点P,Q同时从A出发向点E运动,P的速度为1单位/秒,Q的速度为2单位/秒,当Q到达E时,两点同时停止运动,设t秒后,PQ+QM的值最小,求此最小值和t.
如图四边形ABCD,∠B=∠C=90°,AB=BC=4,△AED为等边三角形,M为AB中点,E为BC上一点,动点P,Q同时从A出发向点E运动,P的速度为1单位/秒,Q的速度为2单位/秒,当Q到达E时,两点同时停止运动,设t秒后,PQ+QM的值最小,求此最小值和t. 分析 如图,作AM⊥CD于K,连接AC,作QG⊥AC于G,作MN⊥AC于N交AE于Q′,首先证明Rt△ADK≌Rt△AEB,推出∠DAK=∠BAE,推出∠DAK=∠BAE=15°,由∠CAE=∠CAB-∠BAE=30°,推出GQ=$\frac{1}{2}$AQ,由PQ=2t-t=t=$\frac{1}{2}$AQ,推出PQ=GQ,所以MQ+PQ=MQ+GQ,所以当G、Q、M共线时,MQ+QP的值最小,由此即可解决问题.
解答 解:如图,作AM⊥CD于K,连接AC,作QG⊥AC于G,作MN⊥AC于N交AE于Q′.
∵∠K=∠KCB=∠B=90°,
∴四边形ABCK是矩形,
∵AB=BC,
∴四边形ABCK是正方形,
∴AB=AK,∵AD=AE,
∴Rt△ADK≌Rt△AEB,
∴∠DAK=∠BAE,
∵∠DAE=60°,∠KAB=90°,
∴∠DAK=∠BAE=15°,
∴∠CAE=∠CAB-∠BAE=30°,
∴GQ=$\frac{1}{2}$AQ,
∵PQ=2t-t=t=$\frac{1}{2}$AQ,
∴PQ=GQ,
∴MQ+PQ=MQ+GQ,
∴当G、Q、M共线时,MQ+QP的值最小,
此时MQ+QG的最小值=MQ′+Q′N=MN,
在Rt△AMN中,∵∠NAM=∠NMA=45°,AM=2,
∴MN=$\sqrt{2}$,
∴PQ+QM的最小值为$\sqrt{2}$.此时AQ′=2NQ′=2×$\sqrt{2}$×$\frac{\sqrt{3}}{3}$=$\frac{2\sqrt{6}}{3}$,
∴2t=$\frac{2\sqrt{6}}{3}$,
∴此时t=$\frac{\sqrt{6}}{3}$s.
点评 本题考查正方形的性质、垂线段最短等知识,解题的关键是学会用转化是思想思考问题,把问题转化为垂线段最短问题,题目比较难,所以中考压轴题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相等 | B. | 互为相反数 | C. | 互为倒数 | D. | 互为负倒数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com