
【题目】一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
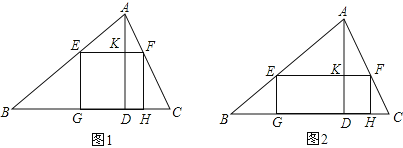
(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长;
(3)如果把它加工成矩形零件如图2,问这个矩形的最大面积是多少?
【答案】(1)证明见解析;(2)48;(3)2400.
【解析】
试题分析:(1)根据矩形的对边平行得到BC∥EF,利用“平行于三角形的一边的直线截其他两边或其他两边的延长线,得到的三角形与原三角形相似”判定即可.
(2)根据正方形边的平行关系,得出对应的相似三角形,即△AEF∽△ABC,△BFG∽△BAD,从而得出边长之比![]() =
=![]() ,
,![]() =
=![]() ,得到
,得到![]() +
+![]() =
=![]() +
+![]() =1,进而求出正方形的边长;
=1,进而求出正方形的边长;
(3)分别讨论长方形的长和宽在BC上的情况,再根据相应得关系式EF BC +EG.
试题解析
(1)∵四边形EGFH为矩形,
∴BC∥EF,
∴△AEF∽△ABC;
(2)设正方形零件的边长为x,
在正方形EFGH中,EF∥BC∴△AEF∽△ABC∴![]() 即
即![]() ,
,
解得:x=48,
即:正方形零件的边长为48;
(3)设长方形的长为x,宽为y,
当长方形的长在BC时,![]() ,
,![]() ,
,
![]() ,
,
当x=60时,
长方形的面积最大为2400.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE;⑤CF=BD.正确的有( )个.

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知二次函数![]() .
.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
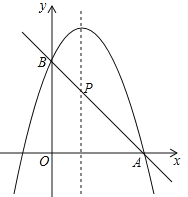
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把自然数按如图的次序排列在直角坐标系中,每个点坐标就对应着一个自然数,例如点(0,0)对应的自然数是1,点(1,2)对应的自然数是14,那么点(1,4)对应的自然数是____;点(n,n)对应的自然数是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,点D是直线AB上一点,延长CB到点E,使BE=AD,连接DE,DC,
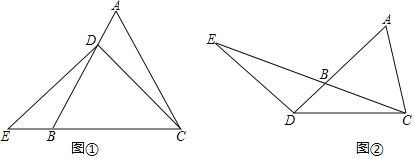
(1)若点D在线段AB上,且AB=6,AD=2(如图①),求证:DE=DC;并求出此时CD的长;
(2)若点D在线段AB的延长线上,(如图②),此时是否仍有DE=DC?请证明你的结论;
(3)在(2)的条件下,连接AE,若![]() ,求CD:AE的值.
,求CD:AE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地某月1~20日中午12时的气温(单位:℃)如下:
22 31 25 15 18 23 21 20 27 17 20 12 18 21 21 16 20 24 26 19
(1)将下列频数分布表补充完整:
气温分组 | 划记 | 频数 |
12≤x<17 |
| 3 |
17≤x<22 |
| 10 |
22≤x<27 |
| 5 |
27≤x<32 |
| 2 |

(2)补全频数分布直方图;
(3)根据频数分布表或频数分布直方图,分析数据的分布情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△P1OA1,△P2A1A2,△P3A2A3,…都是等腰直角三角形,其直角顶点P1(3,3),P2,P3,…均在直线y=﹣![]() x+4上,设△P1OA1,△P2A1A2,△P3A2A3,…的面积分别为S1,S2,S3,…依据图形所反映的规律,S2019=_____.
x+4上,设△P1OA1,△P2A1A2,△P3A2A3,…的面积分别为S1,S2,S3,…依据图形所反映的规律,S2019=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后D的对应点D2的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com