
【题目】已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:①该抛物线的对称轴在y轴左侧;②关于x的方程ax2+bx+c+2=0无实数根;③a﹣b+c≥0; ④ ![]() 的最小值为3.其中正确的是( )
的最小值为3.其中正确的是( )
A.①②③
B.②③④
C.①③④
D.①②③④
【答案】D
【解析】解:∵b>a>0, ∴抛物线的对称轴x=﹣ ![]() <0,所以①正确;
<0,所以①正确;
∵抛物线与x轴最多有一个交点,
而抛物线开口向上,
∴关于x的方程ax2+bx+c=﹣2无实数根,所以②正确;
∵a>0及抛物线与x轴最多有一个交点,
∴x取任何值时,y≥0,
∴当x=﹣1时,a﹣b+c≥0;所以③正确;
当x=﹣2时,y=4a﹣2b+c≥0,
∴a+b+c≥3b﹣3a,
即a+b+c≥3(b﹣a),
而b>a>0,
∴ ![]() ≥3,所以④正确.
≥3,所以④正确.
故选D.
利用抛物线的对称轴方程x=﹣ ![]() <0可对①进行判断;抛物线与x轴最多有一个交点且抛物线开口向上,则y≥0,则可对②③进行判断;当x=﹣2时,y=4a﹣2b+c≥0,变形得到 a+b+c≥3(b﹣a),则利用b>a>0得到
<0可对①进行判断;抛物线与x轴最多有一个交点且抛物线开口向上,则y≥0,则可对②③进行判断;当x=﹣2时,y=4a﹣2b+c≥0,变形得到 a+b+c≥3(b﹣a),则利用b>a>0得到 ![]() ≥3,则可对D进行判断.
≥3,则可对D进行判断.


科目:初中数学 来源: 题型:
【题目】如图,OABC是平行四边形,对角线OB在轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y= ![]() 和y=
和y= ![]() 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
① ![]() =
= ![]() ;
;
②阴影部分面积是 ![]() (k1+k2);
(k1+k2);
③当∠AOC=90°时,|k1|=|k2|;
④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.
其中正确的结论是(把所有正确的结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.如图,某天该深潜器在海面下2000米的A点处作业,测得俯角为30°正前方的海底C点处有黑匣子信号发出.该深潜器受外力作用可继续在同一深度直线航行3000米后,再次在B点处测得俯角为45°正前方的海底C点处有黑匣子信号发出,请通过计算判断“蛟龙”号能否在保证安全的情况下打捞海底黑匣子.(参考数据 ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为 cm2 . (结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,M、N分别是边AB、AC的中点,在射线MN上取点D,使∠ADM=∠BAC,连接AD.
(1)如图1,当BC=3时,求DM的长.
(2)如图2,以AB为底边在AB的左侧作等腰△ABE,并且使顶角∠AEB=2∠BAC,连接EM.
①判断四边形AEMD的形状,并说明理由.
②设BC=x(x>0),四边形AEMD的面积为y,试用含x的式子表示y,并说明是否存在x的值,使得四边形AEMD的面积等于△ABC的面积?若存在,请求出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强公路的节水意识,合理利用水资源,某市对居民用水实行阶梯水价,居民家庭每月用水量划分为两个阶梯,一、二阶梯用水的单价之比等于1:2,如图折线表示实行阶梯水价后每月水费y(元)与用水量x(m3)之间的函数关系,其中射线AB表示第二级阶梯时y与x之间的函数关系. 
(1)写出点B的实际意义;
(2)求射线AB所在直线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
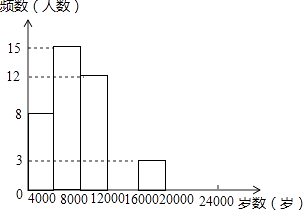
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,D为 ![]() 的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E.
的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E. 
(1)求证:DE是⊙O的切线;
(2)连接CD,若OA=AE=4,求四边形ACDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知λ∈R,函数f(x)=ex﹣ex﹣λ(xlnx﹣x+1)的导数为g(x).
(1)求曲线y=f(x)在x=1处的切线方程;
(2)若函数g(x)存在极值,求λ的取值范围;
(3)若x≥1时,f(x)≥0恒成立,求λ的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com