
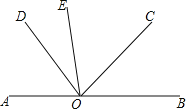
【题目】如图,已知,A、O、B在同一条直线上,∠AOE=∠COD,∠EOD=30°.
(1)若∠AOE=88°30′,求∠BOC的度数;
(2)若射线OC平分∠EOB,求∠BOC的度数.
【答案】(1) 33°;(2) ∠BOC=50°
【解析】
(1)先求出∠AOC度数,再利用∠AOC与∠BOC互补关系求解;
(2)由∠AOE=∠COD,易得∠AOD=∠COE,再借助角平分线定义分析出∠AOD=∠COE=∠BOC,根据这三个等角加上∠DOE等于180°列方程,从而可求出∠BOC度数.
(1)∵∠AOC=∠AOE+∠DOC-∠DOE =88°30′+88°30′-30°=147°,
∴∠BOC=180°-∠AOC =180°-147°=33°;
(2)∵∠AOE=∠COD,
∴∠AOE-∠DOE=∠COD-∠DOE,
即∠AOD=∠COE,
∵OC平分∠BOE,
∴∠BOC=∠COE,
∴∠BOC=∠COE=∠AOD,
设∠BOC=∠COE=∠AOD=x°,
则3x+30°=180°,解得x=50°,
所以∠BOC=50°.


科目:初中数学 来源: 题型:
【题目】如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.( ![]() =1.732,结果精确到0.1米)
=1.732,结果精确到0.1米)
DEB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,顶点M关于x轴的对称点是M′.
(1)求抛物线的解析式;
(2)若直线AM′与此抛物线的另一个交点为C,求△CAB的面积;
(3)是否存在过A,B两点的抛物线,其顶点P关于x轴的对称点为Q,使得四边形APBQ为正方形?若存在,求出此抛物线的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑电瓶车,乙骑自行车从相距17km的两地相向而行.
(1)甲、乙同时出发经过0.5h相遇,且甲每小时行程是乙每小时行程的3倍少6km.求乙骑自行车的速度.
(2)若甲、乙骑行速度保持与(1)中的速度相同,乙先出发0.5h,甲才出发,问甲出发几小时后两人相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要得到△ABD≌△ACE,从下列条件中补选一个,则错误的是( )

A.AB=AC B.DB=EC C.∠ADB=∠AEC D.∠B=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机构对2016年微信用户的职业颁布进行了随机抽样调查(职业说明:A:党政机关、军队,B:事业单位,C:企业,D:自由职业及人体户,E:学生,F:其他),图1和图2是根据调查数据绘制而成的不完整的统计图.请根据图中提供的信息,解答下列问题: 
(1)该机构共抽查微信用户人;
(2)在图1中,补全条形统计图;
(3)在图2中,“D”用户所对应扇形的圆心角度数为度;
(4)2016年微信用户约有7.5亿人,估计“E”用户大约有亿人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次期中考试中A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示:
A | B | C | D | E | 平均分 | 标准差 | |
数学 | 71 | 72 | 69 | 68 | 70 |
| |
英语 | 88 | 82 | 94 | 85 | 76 | 85 |
【1】求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
【2】为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是标准分=(个人成绩-平均成绩)÷成绩标准差. 从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知PA、PB切⊙O于A,B两点,连AB,且PA,PB的长是方程x2﹣2mx+3=0的两根,AB=m.试求: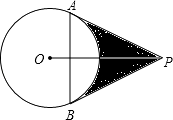
(1)⊙O的半径;
(2)由PA,PB, ![]() 围成图形(即阴影部分)的面积.
围成图形(即阴影部分)的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com