
分析 (1)根据直线y=mx-m+4=(x-1)m+4无论m为何值恒过点C,可得点C坐标,再代入y=$\frac{k}{x}$即可得k的值;
(2)根据点到直线距离公式整理可得(d2-1)m2+8m+d2-16=0,再由△≥0,即82-4(d2-1)(d2-16)≥0可求得d的范围,从而得出答案.
解答 解:(1)∵直线y=mx-m+4=(x-1)m+4无论m为何值恒过点C,
∴当x=1时,y=4,即点C坐标为(1,4),
将点C(1,4)代入y=$\frac{k}{x}$,得k=4,
故答案为:4.
(2)∵原点O到直线AB:y=mx-m+4的距离d=$\frac{|4-m|}{\sqrt{{m}^{2}+1}}$,
∴整理可得(d2-1)m2+8m+d2-16=0,
由△=82-4(d2-1)(d2-16)≥0,可得0≤d2≤17,
∴0≤d≤$\sqrt{17}$,即原点O到直线AB的最大距离是$\sqrt{17}$,
故答案为:$\sqrt{17}$.
点评 本题主要考查反比例函数与一次函数的交点问题及点到直线的距离公式,根据直线横过定点得出C的坐标及熟记距离公式是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
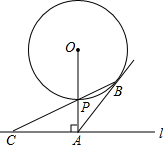 如图,已知直线l与⊙O相离,OA⊥l于点A,OA与⊙O相交于点P,点B为⊙O上一点,BP的延长线交直线l于点C,且 AB=AC.
如图,已知直线l与⊙O相离,OA⊥l于点A,OA与⊙O相交于点P,点B为⊙O上一点,BP的延长线交直线l于点C,且 AB=AC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
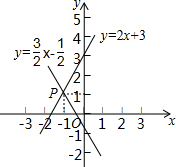 如图,函数y=-$\frac{3}{2}$x-$\frac{1}{2}$和y=2x+3的图象交于点P,则根据图象可得,二元一次方程组$\left\{\begin{array}{l}{y=2x+3}\\{y=-\frac{3}{2}x-\frac{1}{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$.
如图,函数y=-$\frac{3}{2}$x-$\frac{1}{2}$和y=2x+3的图象交于点P,则根据图象可得,二元一次方程组$\left\{\begin{array}{l}{y=2x+3}\\{y=-\frac{3}{2}x-\frac{1}{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 进货价/(元/箱) | 出售加价率 | |
| A种酸奶 | 16 | 20% |
| B种酸奶 | 20 | 25% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,CD为⊙O的直径,弦AB交CD于点E,连接BD、OB.
如图,CD为⊙O的直径,弦AB交CD于点E,连接BD、OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
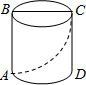 如图:一个圆柱的底面周长为16cm,高为6cm,BC是上底面的直径,一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,求蚂蚁爬行的最短路程(要求画出平面图形).
如图:一个圆柱的底面周长为16cm,高为6cm,BC是上底面的直径,一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,求蚂蚁爬行的最短路程(要求画出平面图形).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
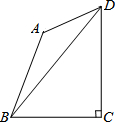 如图,四边形ABCD中,∠BAD=135°,∠BCD=90°,AB=BC=4,tan∠BDC=$\frac{\sqrt{6}}{3}$.
如图,四边形ABCD中,∠BAD=135°,∠BCD=90°,AB=BC=4,tan∠BDC=$\frac{\sqrt{6}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com