
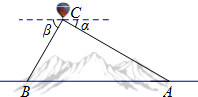
 2014年11月25日,国家发改委批准了我省三条泛亚铁路的规划和建设计划.为加快勘测设计,某勘测部门使用了热气球对某隧道的长进行勘测.如图所示,热气球C的探测器显示,从热气球观测隧道入口A的俯角α为30°,观测隧道出口B的俯角β为60°,热气球相对隧道的飞行高度为1200m,求这条隧道AB的长?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留2位小数)
2014年11月25日,国家发改委批准了我省三条泛亚铁路的规划和建设计划.为加快勘测设计,某勘测部门使用了热气球对某隧道的长进行勘测.如图所示,热气球C的探测器显示,从热气球观测隧道入口A的俯角α为30°,观测隧道出口B的俯角β为60°,热气球相对隧道的飞行高度为1200m,求这条隧道AB的长?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留2位小数) 分析 过点C作CD⊥AB于点D,根据已知条件和特殊角的三角函数值求出BD和AD的值,再根据AB=BD+AD,即可得出答案.
解答 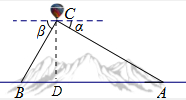 解:过点C作CD⊥AB于点D,
解:过点C作CD⊥AB于点D,
由题意知:∠BCD=30°,∠ACD=60°,CD=1200,
在Rt△CDB和Rt△CDA中,
∵tan30°=$\frac{BD}{CD}$,tan60°=$\frac{AD}{CD}$,
∴BD=CD•tan30°=400$\sqrt{3}$,
AD=CD•tan60°=1200$\sqrt{3}$,
∴AB=BD+AD=400$\sqrt{3}$+1200$\sqrt{3}$=1600$\sqrt{3}$≈2771(m).
答:这条隧道的长约为2771m.
点评 本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
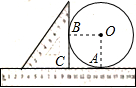 如图,圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺的10cm处,铁片与直尺的唯一公共点A落在直尺的14cm处,铁片与三角尺的唯一公共点为B,下列说法错误的是( )
如图,圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺的10cm处,铁片与直尺的唯一公共点A落在直尺的14cm处,铁片与三角尺的唯一公共点为B,下列说法错误的是( )| A. | 圆形铁片的半径是4cm | B. | 四边形AOBC为正方形 | ||
| C. | 弧AB的长度为4πcm | D. | 扇形OAB的面积是4πcm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com