
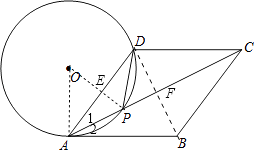
【题目】如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆. 
(1)求证:AB是⊙O的切线;
(2)若AC=8,tan∠BAC= ![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】
(1)解:连结OP、OA,OP交AD于E,如图,
∵PA=PD,
∴弧AP=弧DP,
∴OP⊥AD,AE=DE,
∴∠1+∠OPA=90°,
∵OP=OA,
∴∠OAP=∠OPA,
∴∠1+∠OAP=90°,
∵四边形ABCD为菱形,
∴∠1=∠2,
∴∠2+∠OAP=90°,
∴OA⊥AB,
∴直线AB与⊙O相切;
(2)解:连结BD,交AC于点F,如图,
∵四边形ABCD为菱形,
∴DB与AC互相垂直平分,
∵AC=8,tan∠BAC= ![]() ,
,
∴AF=4,tan∠DAC= ![]() =
= ![]() ,
,
∴DF=2 ![]() ,
,
∴AD= ![]() =2
=2 ![]() ,
,
∴AE= ![]() ,
,
在Rt△PAE中,tan∠1= ![]() =
= ![]() ,
,
∴PE= ![]() ,
,
设⊙O的半径为R,则OE=R﹣ ![]() ,OA=R,
,OA=R,
在Rt△OAE中,∵OA2=OE2+AE2,
∴R2=(R﹣ ![]() )2+(
)2+( ![]() )2,
)2,
∴R= ![]() ,
,
即⊙O的半径为 ![]() .
.
【解析】(1)连结OP、OA,OP交AD于E,由PA=PD得弧AP=弧DP,根据垂径定理的推理得OP⊥AD,AE=DE,则∠1+∠OPA=90°,而∠OAP=∠OPA,所以∠1+∠OAP=90°,再根据菱形的性质得∠1=∠2,所以∠2+∠OAP=90°,然后根据切线的判定定理得到直线AB与⊙O相切;(2)连结BD,交AC于点F,根据菱形的性质得DB与AC互相垂直平分,则AF=4,tan∠DAC= ![]() ,得到DF=2
,得到DF=2 ![]() ,根据勾股定理得到AD=
,根据勾股定理得到AD= ![]() =2
=2 ![]() ,求得AE=
,求得AE= ![]() ,设⊙O的半径为R,则OE=R﹣
,设⊙O的半径为R,则OE=R﹣ ![]() ,OA=R,根据勾股定理列方程即可得到结论.
,OA=R,根据勾股定理列方程即可得到结论.
【考点精析】本题主要考查了菱形的性质和解直角三角形的相关知识点,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数的图象与反比例函数的图象相交于A、B两点。
(1)利用图中的条件,求反比例函数和一次函数的解析式;
(2)根据图象直接写出一次函数的值大于反比例函数的x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,AB∥DC,连接BD,BE平分∠ABD,BE⊥AD,∠EBC和∠DCB的角平分线相交于点F,若∠ADC=110°,则∠F的度数为( )
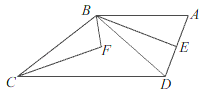
A. 115° B. 110° C. 105° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的个数有( )
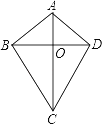
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,点M是BE的中点,连接CM、DM.

(1)当点D在AB上,点E在AC上时(如图一),求证:DM=CM,DM⊥CM;
(2)当点D在CA延长线上时(如图二)(1)中结论仍然成立,请补全图形(不用证明);
(3)当ED∥AB时(如图三),上述结论仍然成立,请加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:
(概念理解)
在一个三角形中,如果一个角的度数是另一个角度数的 4 倍,那么这样的三角形我们称之为“完美三角形”.如:三个内角分别为 130°,40°,10°的三角形是“完美三角形”.
(简单应用)
如图 1,∠MON=72°,在射线OM上找一点A,过点A作AB⊥OM 交ON于点B,以A为端点作射线AD,交线段OB 于点C(点 C不与 O,B重合)
(1)∠ABO= ,△AOB__________(填“是”或“不是”)“完美三角形”;
(2)若∠ACB=90°,求证:△AOC是“完美三角形”.
(应用拓展)
如图 2,点D在△ABC 的边AB上,连接DC,作∠ADC的平分线交AC于点E,在DC上取点F,使![]() ,
,![]() .若△BCD是“完美三角形”, 求∠B的度数.
.若△BCD是“完美三角形”, 求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两个工程队共同修建一条公路,从两端同时开始,到工程结束时,甲工程 队共施工了![]() 天,乙队在中途接到紧急任务停止施工一段时间,回来后按照以前的施工 速度继续施工至结束,设甲、乙两工程队各自施工的长度分別为
天,乙队在中途接到紧急任务停止施工一段时间,回来后按照以前的施工 速度继续施工至结束,设甲、乙两工程队各自施工的长度分別为![]() (米),
(米),![]() (米),甲 队施工的时间为
(米),甲 队施工的时间为![]() (天),
(天),![]() ,
,![]() 与
与![]() 之间的函数图象如图所示.
之间的函数图象如图所示.
(1)这条公路的总长度是______米;
(2)求乙队在恢复施工后,![]() 与
与![]() 之间的函数表 达式;
之间的函数表 达式;
(3)求在修建该条公路的过程中,甲、乙两队共同修建完![]() 米长时甲队施工的天数.
米长时甲队施工的天数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与坐标轴分别交于
与坐标轴分别交于![]() ,
,![]() 两点,以线段
两点,以线段![]() 为边,在第一象限内作正方形
为边,在第一象限内作正方形![]() ,将正方形
,将正方形![]() 沿
沿![]() 轴负方向,平移
轴负方向,平移![]() 个单位长度,使点
个单位长度,使点![]() 恰好落在直线
恰好落在直线![]() 上,则
上,则![]() 的值为________.
的值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为解决部分市民冬季集中取暖问题需铺设一条长3000米的管道,为尽量减少施工对交通造成的影响,实施施工时“…”,设实际每天铺设管道x米,则可得方程 ![]() ,根据此情景,题中用“…”表示的缺失的条件应补为( )
,根据此情景,题中用“…”表示的缺失的条件应补为( )
A.每天比原计划多铺设10米,结果延期15天才完成
B.每天比原计划少铺设10米,结果延期15天才完成
C.每天比原计划多铺设10米,结果提前15天才完成
D.每天比原计划少铺设10米,结果提前15天才完成
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com