
数学课上,老师出示如图和下面框中条件,

同学发现两个结论:①S△CMD∶S梯形ABMC=2∶3;
②数值相等关系:xC·xD=-yH.

(1)请你验证结论①和结论②成立;
(2)请你研究:如果将上述框中的条件“A点坐标为(1,0)”改为“A点坐标为(t,0),(t>0)”.其他条件不变,结冰①是否仍成立?(请说出理由)
(3)进一步研究:如果将上述框中的条件“A点坐标为(1,0)”改为“A点坐标为(t,0)(t>0)”.又将条件“y=x2”改为“y=ax2(a>0)”其他条件不变,那么xC、xD和yH有怎样的数值关系?(写出结果并说明理由)
|
(1)由已知可得点B的坐标为(2,0),点C的坐标为(1,l)点D的坐标为(2,4)由点C坐标为(1,1)易得直线OC的函数解析式为y=x,∴点M的坐标为(2,2),∴S△CMD=1,S梯形ABMC= (2)结论①仍成立.∵点A的坐标为(t,0)(t>0),则点B坐标为(2t,0),从而点C坐标为(t,t2),点D坐标为(2t,4t2),设直线OC的函数解析式为y=kx,则t2=kt,得k=t,∴直线OC的函数解析式为y=tx,设点M的坐标为(2t,y),∵点M在直线OC上,∴当x=2t时,y=2t2,点M的坐标为(2t,2t2),∴S△CMD∶S梯形ABMC= (3)xC·xD=- |


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
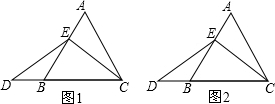 (2013•许昌一模)某次数学课上,老师出示了一道题,如图1,在边长为4等边三角形ABC中,点E在AB上.
(2013•许昌一模)某次数学课上,老师出示了一道题,如图1,在边长为4等边三角形ABC中,点E在AB上.| AE |
| AB |
| 1 |
| 3 |
| 16 |
| 3 |
| 16 |
| 3 |
| AE |
| AB |
| 1 |
| n |
| mn+m |
| n |
| mn+m |
| n |
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题8分)数学课上,老师出示了如下框中的题目.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况•探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的
边长为1,AE=2,求CD的长(请你直接写出结果) .
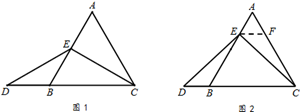 |
查看答案和解析>>
科目:初中数学 来源:浙江省衢州市实验学校2011-2012学年八年级上学期期末考试数学卷 题型:解答题
(本题8分)数学课上,老师出示了如下框中的题目.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况•探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填 “>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的
边长为1,AE=2,求CD的长(请你直接写出结果) .
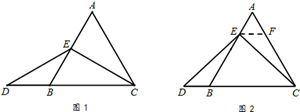 |
查看答案和解析>>
科目:初中数学 来源:浙江省2013届八年级上学期期末考试数学卷 题型:选择题
(本题8分)数学课上,老师出示了如下框中的题目.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况•探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填 “>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的
边长为1,AE=2,求CD的长(请你直接写出结果) .
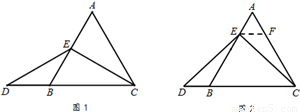 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com