
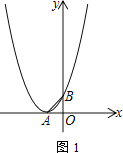
【题目】已知抛物线顶点A在x轴负半轴上,与y轴交于点B,OB=1,△OAB为等腰直角三角形
(1)求抛物线的解析式
(2)若点C在抛物线上,若△ABC为直角三角形,求点C的坐标
(3)已知直线DE过点(-1,-4),交抛物线于点D、E,过D作DF∥x轴,交抛物线于点F,求证:直线EF经过一个定点,并求定点的坐标

【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析,定点
;(3)见解析,定点![]()
【解析】
(1)根据题意可得出点A的坐标,用顶点式求解抛物线解析式即可;
(2)设点C的坐标为(x,y),利用勾股定理的逆定理分三种情况讨论即可;
(3)设![]() 的解析式为
的解析式为![]() ,联立直线DE与抛物线解析式得出
,联立直线DE与抛物线解析式得出![]() ,从而得出
,从而得出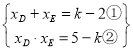 ,继而得出
,继而得出![]() ,再设
,再设![]() 的解析式为
的解析式为![]() ,通过联立得出
,通过联立得出![]() ,进一步得出
,进一步得出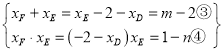 ,联立①②③④得
,联立①②③④得![]() ,所以
,所以![]() ,过定点
,过定点![]()
解:(1)根据题意可得出抛物线顶点的坐标为(-1,0),
∴抛物线的解析式为:![]() ;
;
(2)设点C的坐标为(x,y),![]() ,A(-1,0),B(0,1),
,A(-1,0),B(0,1),
当![]() 为直角顶点时,
为直角顶点时,![]() ,
,
∴![]() ,
,
整理得:![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得:![]() (舍去),
(舍去),
∴![]() ,
,
∴点C的坐标为![]() ;
;
同理,当![]() 为直角顶点时,
为直角顶点时,![]() ,
,
∴![]() ,
,
整理得:![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得:![]() (舍去),
(舍去),
∴![]() ,
,
∴点C的坐标为![]() ;
;
当![]() 为直角顶点时,不存在符合条件的点C;
为直角顶点时,不存在符合条件的点C;
(3)设![]() 的解析式为
的解析式为![]() ,联立
,联立![]() ,
,
得,![]() ,
,
∴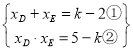 ,
,
∵![]() 、F关于对称轴对称,
、F关于对称轴对称,
∴![]() ,
,
设![]() 的解析式为
的解析式为![]() ,
,
联立![]() ,
,
得,![]() ,
,
∴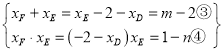 ,
,
联立①②③④得![]() ,
,
∴![]() ,过定点
,过定点![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】某文明小区50平方米和80平方米两种户型的住宅,50平方米住宅套数是80平方米住宅套数的2倍.物管公司月底按每平方米2元收取当月物管费,该小区全部住宅都人住且每户均按时全额缴纳物管费.
(1)该小区每月可收取物管费90 000元,问该小区共有多少套80平方米的住宅?
(2)为建设“资源节约型社会”,该小区物管公司5月初推出活动一:“垃圾分类送礼物”,50平方米和80平方米的住户分别有40%和20%参加了此次括动.为提离大家的积扱性,6月份准备把活动一升级为活动二:“拉圾分类抵扣物管费”,同时终止活动一.经调査与测算,参加活动一的住户会全部参加活动二,参加活动二的住户会大幅增加,这样,6月份参加活动的50平方米的总户数在5月份参加活动的同户型户数的基础上将增加![]() ,每户物管费将会减少
,每户物管费将会减少![]() ;6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加
;6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加![]() ,每户物管费将会减少
,每户物管费将会减少![]() .这样,参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少
.这样,参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲地有42吨货物要运到乙地,有大、小两种货车可供选择,具体收费情况如表:
类型 | 载重量(吨) | 运费(元/车) |
大货车 | 8 | 450 |
小货车 | 5 | 300 |
运完这批货物最少要支付运费_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线 y=ax2 -2ax+4(a<0) 交 x 轴于点 A、B,与 y 轴交于点 C,AB=6.

(1)如图 1,求抛物线的解析式;
(2) 如图 2,点 R 为第一象限的抛物线上一点,分别连接 RB、RC,设△RBC 的面积为 s,点 R 的横坐标为 t,求 s 与 t 的函数关系式;
(3)在(2)的条件下,如图 3,点 D 在 x 轴的负半轴上,点 F 在 y 轴的正半轴上,点 E 为 OB 上一点,点 P 为第一象限内一点,连接 PD、EF,PD 交 OC 于点 G,DG=EF,PD⊥EF,连接 PE,∠PEF=2∠PDE,连接 PB、PC,过点R 作 RT⊥OB 于点 T,交 PC 于点 S,若点 P 在 BT 的垂直平分线上,OB-TS=![]() ,求点 R 的坐标.
,求点 R 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
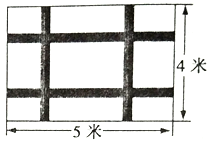
【题目】如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的![]() .
.
(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.
查看答案和解析>>
科目:初中数学 来源: 题型:
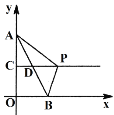
【题目】如图,点A(0,4)、B(2,0),点C、D分别是OA、AB的中点,在射线CD上有一动点P,若△ABP是直角三角形,则点P的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(-1,O)、C(3,0),点B为抛物线顶点,直线BD为抛物线的对称轴,点D在x轴上,连接AB、BC.

⑴如图1,若∠ABC=60°,则点B的坐标为______________;
⑵如图2,若∠ABC=90°,AB与y轴交于点E,连接CE.
①求这条抛物线的解析式;
②点P为第一象限抛物线上一个动点,设△PEC的面积为S,点P的横坐标为m,求S关于m的函数关系武,并求出S的最大值;
③如图3,连接OB,抛物线上是否存在点Q,使直线QC与直线BC所夹锐角等于∠OBD,若存在请直接写出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,已知△ABC中,AC=BC=AB=6,△ABC的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的距离为整数的点有( )个.
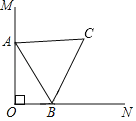
A.5B.6C.7D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同。
(1)从箱子中任意摸出一个球是白球的概率是多少?
(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com