
加工一种产品,需先将材料加热达到60℃后,再停止加热进行加工,设该材料温度为y﹙℃﹚,从加热开始计算的时间为x(分钟).据了解,该材料在加热时,温度y是时间x的一次函数,停止加热进行加工时,温度y与时间x成反比例关系(如图所示),己知该材料在加热前的温度为l5℃,加热5分钟后温度达到60℃.
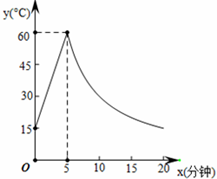
(1)分别求出将材料加热和加工时,y与x的函数关系式(不必写出自变量的取值范围);
(2)根据工艺要求,当材料的温度低于l5℃时,必须停止加工,那么加工时间是多少分钟?
(1)![]() ,
,![]() ;(2)15分钟
;(2)15分钟
【解析】
试题分析:(1)当材料在加热时,温度![]() 是时间
是时间![]() 的一次函数,设一次函数的解析式为
的一次函数,设一次函数的解析式为![]() ,由图象可知一次函数图象经过(0,15),(5,60)根据待定系数法求解即可;当停止加热进行加工时,温度
,由图象可知一次函数图象经过(0,15),(5,60)根据待定系数法求解即可;当停止加热进行加工时,温度![]() 与时间
与时间![]() 成反比例关系,设反比例函数的解析式为
成反比例关系,设反比例函数的解析式为![]() ,由图象可知,反比例函数图象经过(5,60)根据待定系数法求解即可;
,由图象可知,反比例函数图象经过(5,60)根据待定系数法求解即可;
(2)把![]() 代入(1)中的反比例函数的解析式即可求得结果.
代入(1)中的反比例函数的解析式即可求得结果.
解:(1)当材料在加热时,
∵温度![]() 是时间
是时间![]() 的一次函数
的一次函数
∴设一次函数的解析式为![]()
由图象可知,一次函数图象经过(0,15),(5,60)
代入可得:![]() ,解得
,解得![]()
∴![]()
当停止加热进行加工时,
∵温度![]() 与时间
与时间![]() 成反比例关系
成反比例关系
∴设反比例函数的解析式为![]()
由图象可知,反比例函数图象经过(5,60)
代入可得:![]() ,解得
,解得![]()
∴![]() ;
;
(2)当![]() 时,
时,![]() ,解得
,解得![]()
∴加工时间为:![]() 分钟
分钟
答:加工时间是15分钟.
考点:一次函数与反比例函数的综合应用
点评:函数的应用是初中数学的重点,是中考中比较常见的知识点,一般难度不大,需熟练掌握.


科目:初中数学 来源: 题型:
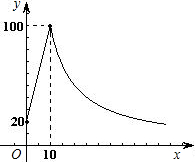 函数,停止加热进行操作时,温度y与时间x成反比例关系(如图所示).
函数,停止加热进行操作时,温度y与时间x成反比例关系(如图所示).查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012-2013学年黑龙江哈尔滨香坊八年级下学期期末调研测试数学试卷(带解析) 题型:解答题
加工一种产品,需先将材料加热达到60℃后,再停止加热进行加工,设该材料温度为y﹙℃﹚,从加热开始计算的时间为x(分钟).据了解,该材料在加热时,温度y是时间x的一次函数,停止加热进行加工时,温度y与时间x成反比例关系(如图所示),己知该材料在加热前的温度为l5℃,加热5分钟后温度达到60℃.
(1)分别求出将材料加热和加工时,y与x的函数关系式(不必写出自变量的取值范围);
(2)根据工艺要求,当材料的温度低于l5℃时,必须停止加工,那么加工时间是多少分钟?
查看答案和解析>>
科目:初中数学 来源:2014届黑龙江哈尔滨香坊八年级下学期期末调研测试数学试卷(解析版) 题型:解答题
加工一种产品,需先将材料加热达到60℃后,再停止加热进行加工,设该材料温度为y﹙℃﹚,从加热开始计算的时间为x(分钟).据了解,该材料在加热时,温度y是时间x的一次函数,停止加热进行加工时,温度y与时间x成反比例关系(如图所示),己知该材料在加热前的温度为l5℃,加热5分钟后温度达到60℃.
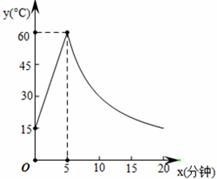
(1)分别求出将材料加热和加工时,y与x的函数关系式(不必写出自变量的取值范围);
(2)根据工艺要求,当材料的温度低于l5℃时,必须停止加工,那么加工时间是多少分钟?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com