
【题目】如图,![]() 的对角线
的对角线![]() 交于点
交于点![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() :④
:④![]() 其中正确的结论有__________(填写所有正确结论的序号)
其中正确的结论有__________(填写所有正确结论的序号)
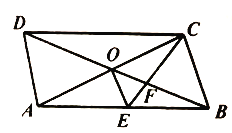
【答案】①③④
【解析】
由四边形ABCD是平行四边形,∠ABC=60°,EC平分∠DCB,得△ECB是等边三角形,结合AB=2BC,得∠ACB=90°,进而得∠CAB=30°,即可判断①;由∠OCF<∠DAO,∠OFC>∠ADO,即可判断②;易证△OEF∽△BCF,得OF=![]() OB,进而得S△AOD=S△BOC=3S△OCF,即可判断③;设OF=a,得DF=4a,BF=2a,即可判断④.
OB,进而得S△AOD=S△BOC=3S△OCF,即可判断③;设OF=a,得DF=4a,BF=2a,即可判断④.
∵四边形ABCD是平行四边形,
∴CD∥AB,OD=OB,OA=OC,
∴∠DCB+∠ABC=180°,
∵∠ABC=60°,
∴∠DCB=120°,
∵EC平分∠DCB,
∴∠ECB=![]() ∠DCB=60°,
∠DCB=60°,
∴∠EBC=∠BCE=∠CEB=60°,
∴△ECB是等边三角形,
∴EB=BC= EC,
∵AB=2BC,
∴EA=EB=EC,
∴∠ACB=90°,
∴∠CAB=30°,即:![]() ,
,
故①正确;
∵AD∥BC,
∴∠ADO=∠CBO,∠DAO=∠BCO,
∵∠OCF<∠BCO,∠OFC>∠CBO,
∴∠OCF<∠DAO,∠OFC>∠ADO,
∴![]() 错误,
错误,
故②错误;
∵OA=OC,EA=EB,
∴OE∥BC,
∴△OEF∽△BCF,
∴![]() ,
,
∴OF=![]() OB,
OB,
∴S△AOD=S△BOC=3S△OCF,
故③正确;
设OF=a,
∵OF=![]() OB,
OB,
∴OB=OD=3a,
∴DF=4a,BF=2a,
∴BF2=OFDF,
故④正确;
故答案为:①③④.


科目:初中数学 来源: 题型:
【题目】已知如图所示,在Rt△ABC中,∠A=90°,∠BCA=75°,AC=8cm,DE垂直平分BC,则BE的长是( )

A.4cmB.8cmC.16cmD.32cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
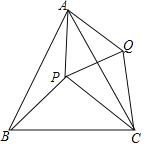
(1)求证:△BAP≌△CAQ.
(2)若PA=3,PB=4,∠APB=150°,求PC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为圆内接四边形,对角线AC、BD交于点E,延长DA、CB交于点F.
(1)求证:△FBD∽△FAC;
(2)如果BD平分∠ADC,BD=5,BC=2,求DE的长;
(3)如果∠CAD=60°,DC=DE,求证:AE=AF.
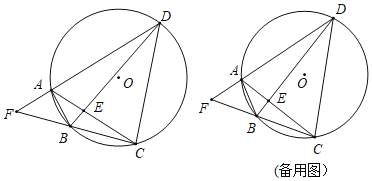
查看答案和解析>>
科目:初中数学 来源: 题型:
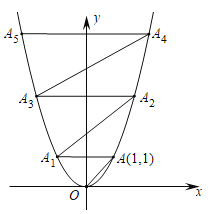
【题目】在平面直角坐标系中, 抛物线![]() 如图所示.已知
如图所示.已知![]() 点的坐标为
点的坐标为![]() ,过点
,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,过点
,过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,过点
,过点![]() 作
作![]() 轴交抛物线于
轴交抛物线于![]() 点,过点
点,过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() …若依次进行下去,则点
…若依次进行下去,则点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D为BC的中点,经过AD两点的圆分别与AB,AC交于点E、F,连接DE,DF.
(1)求证:DE=DF;
(2)求证:以线段BE+CF,BD,DC为边围成的三角形与△ABC相似,
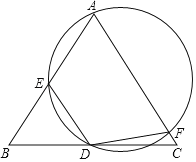
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c的对称轴为直线x=2,且顶点在x轴上.
(1)求b、c的值;
(2)画出抛物线的简图并写出它与y轴的交点C的坐标;
(3)根据图象直接写出:点C关于直线x=2对称点D的坐标 ;若E(m,n)为抛物线上一点,则点E关于直线x=2对称点的坐标为 (用含m、n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() 在
在![]() 边上,以
边上,以![]() 为直径的半圆
为直径的半圆![]() 经过点
经过点![]() ,交
,交![]() 于点
于点![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)已知![]() ,
,![]() 的半径为
的半径为![]() ,求图中阴影部分的面积.(最后结果保留根号和
,求图中阴影部分的面积.(最后结果保留根号和![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com