
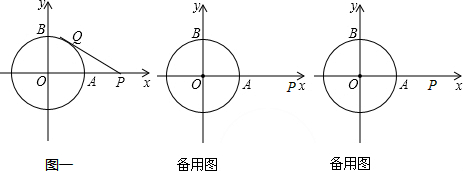
分析 (1)连接OQ,求出∠QPO,求出∠BOQ,根据弧长公式求出即可;
(2)①分为四种情况,画出图形,求出弧长,即可求出答案;
②作OM⊥PQ,根据面积公式即可求出答案.
解答  解:(1)如图1,连接OQ,则OQ⊥PQ.
解:(1)如图1,连接OQ,则OQ⊥PQ.
∵OQ=OA=1,OP=2,
∴∠QPO=30°,
∵∠PQO=90°,
∴∠QOP=60°,
∴∠BOQ=30°,
∴弧BQ的长是$\frac{30π×1}{180}$=$\frac{1}{6}$π,
∵运动时间t=1,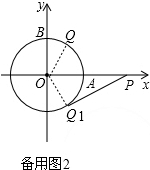
∴点Q的运动速度为$\frac{1}{6}$π;
(2)①分为四种情况:
a、由(1)可知,当t=1时,△OPQ为直角三角形;
b、如备用图2,当点Q1关于x轴对称时,
△OPQ1为直角三角形,此时∠BOQ1=150°,
弧BQ1=$\frac{5}{6}$π,则t=5;
c、当点Q2(0,-1)或Q3(0,1)时,∠POQ2=∠POQ3=90°,
此时t=6或t=12.
即当t=1,t=5,t=6或t=12时,△OPQ为直角三角形;
②如备用图3,当t=6或t=12时,直线PQ与⊙O相交,设交点为N,
作OM⊥PQ,根据等面积法可知:PQ•OM=OQ•OP,
PQ=$\sqrt{O{P}^{2}+O{Q}^{2}}$=$\sqrt{5}$,OM=$\frac{2\sqrt{5}}{5}$,
PM=$\sqrt{O{Q}^{2}-O{M}^{2}}$=$\frac{\sqrt{5}}{5}$,
弦长PN=2PM=$\frac{2\sqrt{5}}{5}$(cm).
点评 本题考查了弧长的计算,三角形面积公式,切线的性质,含30度角的直角三角形性质等知识点的应用,主要考查学生的计算能力,用了分类讨论思想.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
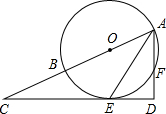 如图,AB为⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.
如图,AB为⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
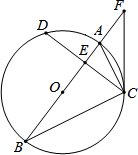 如图,在⊙O中,直径AB平分弦CD,AB与CD相交于点E,连接AC、BC,点F是BA延长线上的一点,且∠FCA=∠B.
如图,在⊙O中,直径AB平分弦CD,AB与CD相交于点E,连接AC、BC,点F是BA延长线上的一点,且∠FCA=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 打开电视机,正在播放广告这一事件是随机事件 | |
| B. | 要了解小红一家三口的身高,适合采用抽样调查 | |
| C. | 方差越大,数据的波动越大 | |
| D. | 样本中个本的数目称为样本容量 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com