
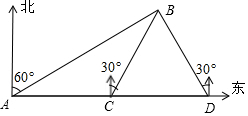
 如图,某货轮上午8时20分从A处出发,此时观测到海岛B的方位为北偏东60°,该货轮以每小时30海里的速度向东航行到C处,此时观测到海岛B的方位为北偏东30°,继续向东航行到D处,观测到海岛B的方位为北偏西30°.当货轮到达C处时恰好与海岛B相距60海里,求该货轮到到达C,D处的时间.
如图,某货轮上午8时20分从A处出发,此时观测到海岛B的方位为北偏东60°,该货轮以每小时30海里的速度向东航行到C处,此时观测到海岛B的方位为北偏东30°,继续向东航行到D处,观测到海岛B的方位为北偏西30°.当货轮到达C处时恰好与海岛B相距60海里,求该货轮到到达C,D处的时间. 分析 根据题意,求得已知角的度数,根据特殊角的三角函数值求得AC、BC的值,从而求得CD的值,根据行程问题的求法再求轮船到达C处和D处的时间即可.
解答 解:由己知,得∠BAC=30°,∠ACB=120°,∠BCD=∠BDC=60°
∴∠ABC=∠BAC=30°
∴AC=BC=60(海里)∠CBD=60°
∴t1=60÷30=2(小时)
∴△BCD是等边三角形∴BC=CD=60(海里)
∴t2=60÷30=2(小时),
∴t3=2+2=4(小时).
答:轮船到达C处是上午10时20分,轮船到达D处的时间是下午12时20分.
或轮船到达C处用了2小时,到达D处用了4小时.
点评 此题是一道方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
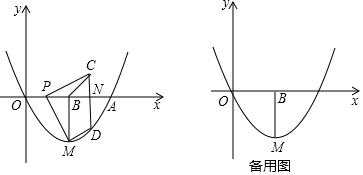
 如图,在正方形ABCD中,对角线AD,BC交于点O,点E、F分别在AC,CD边上,EF∥AD,交BC于点P,若点O是△BEF的重心.
如图,在正方形ABCD中,对角线AD,BC交于点O,点E、F分别在AC,CD边上,EF∥AD,交BC于点P,若点O是△BEF的重心.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 每段绳子长$\frac{25}{30}$米 | B. | 每段绳子占全长的$\frac{6}{7}$ | ||
| C. | 每段绳子长$\frac{6}{7}$米 | D. | 每段绳子是全长的$\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
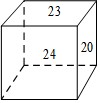 如图,已知一个正方体的六个面上分别写着六个连续的正整数,且每个相对面上的两个数的和都相等,图中所能看到的数是20,23和24,求这六个正整数的和.
如图,已知一个正方体的六个面上分别写着六个连续的正整数,且每个相对面上的两个数的和都相等,图中所能看到的数是20,23和24,求这六个正整数的和.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
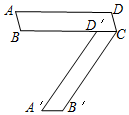 将平行四边形ABCD(如图)绕点C旋转后,点D落在边BC上的点D′,点A落到A′,且点A′、B、A在一直线上.如果AB=3,AD=13,那么cos A=$\frac{5}{13}$.
将平行四边形ABCD(如图)绕点C旋转后,点D落在边BC上的点D′,点A落到A′,且点A′、B、A在一直线上.如果AB=3,AD=13,那么cos A=$\frac{5}{13}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com