
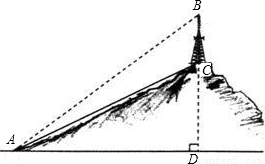
 5、如图,要测量小山上电视塔BC的高度,从山脚下A点测得AC=820m,塔顶B的仰角α=30°,山坡的倾角β=18°,求电视塔的高(精确到1m).
5、如图,要测量小山上电视塔BC的高度,从山脚下A点测得AC=820m,塔顶B的仰角α=30°,山坡的倾角β=18°,求电视塔的高(精确到1m).

 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
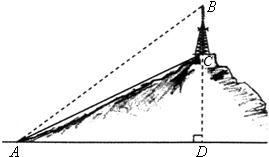 20、如图,要测量小山上电视塔BC的高度,在山脚下点A测得:塔顶B的仰角为∠BAD=40°,塔底C的仰角为∠CAD=29°,AC=200米,求电视塔BC的高.(精确到1米)(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin29°≈0.48,cos29°≈0.87,tan29°≈0.55.)
20、如图,要测量小山上电视塔BC的高度,在山脚下点A测得:塔顶B的仰角为∠BAD=40°,塔底C的仰角为∠CAD=29°,AC=200米,求电视塔BC的高.(精确到1米)(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin29°≈0.48,cos29°≈0.87,tan29°≈0.55.)查看答案和解析>>
科目:初中数学 来源:第4章《锐角三角形》中考题集(35):4.3 解直角三角形及其应用(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第25章《解直角三角形》常考题集(15):25.3 解直角三角形(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:第25章《解直角三角形》常考题集(16):25.3 解直角三角形及其应用(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com