
阅读理解:我们知道:若x![]() = 4,则x=2或x=-2. 因此,小伟在解方程x
= 4,则x=2或x=-2. 因此,小伟在解方程x![]() +2x-8=
+2x-8=![]() 0时
0时![]() ,采用了以下的方法:
,采用了以下的方法:
解:移项,得x![]() +2x=8.
+2x=8.
两边都加上l,得x![]() +2x+1=8+1,∴ (x+1) 2=9.
+2x+1=8+1,∴ (x+1) 2=9.
则x+1=3或x+1=-3. 所以x=2或x=-4.
小伟的这种解方程的方法,在数学上称之为配方法.
拓展应用:请用配方法,解方程x![]() -6x-7=0.
-6x-7=0.
科目:初中数学 来源: 题型:阅读理解
 阅读理解:
阅读理解:| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| n(n-1) |
| 2 |
| n(n-1) |
| 2 |
| (n+1)(n+2) |
| 2 |
| (n+1)(n+2) |
| 2 |
查看答案和解析>>
科目:初中数学 来源:第23章《旋转》中考题集(13):23.2 中心对称(解析版) 题型:解答题
 阅读理解:
阅读理解: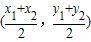 .
.查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《平面直角坐标系》(02)(解析版) 题型:解答题
 (2010•内江)阅读理解:
(2010•内江)阅读理解: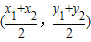 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com