
【题目】在△ABC 中,AB=AC,D 是直线 BC 上一点(不与点 B、C 重合),以 AD 为一边在 AD的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接 CE.
(1)如图 1,当点 D 在线段 BC 上时,求证:△ABD≌△ACE;
(2)如图 2,当点 D 在线段 BC 上时,如果∠BAC=90°,求∠BCE 的度数;
(3)如图 3,若∠BAC=α,∠BCE=β.点 D 在线段 CB 的延长线上时,则α、β之间有怎样 的数量关系?并证明你的结论.



【答案】(1)见解析;(2)90;(3)
【解析】(1)首先求出∠BAD=∠CAE,再利用SAS得出△ABD≌△ACE即可;
(2)由ABAC,BAC90,推出∠ABDACB45 ,由ABD≌ACE,得到∠ABDACE,等量代换得到∠ABDACE,即可求出∠BCE;
(3)当D在CB的延长线上时,α=β,求出∠BAD=∠CAE.推出△ADB和△AEC,推出∠BAC=∠BCE.根据三角形外角性质求出即可.
(1)∵∠DAE=∠BAC ,
∠BAD=∠EAC
∵在△ABD和△ACE中,
AB AC,∠BAD=∠CAE,AD=AE,
ABD≌ACE SAS ;
(2)∵AB AC,BAC 90 ,
∠ABDACB 45 ,
∵ABD≌ACE ,
∠ABDACE,
∠ABDACE,
∠BCEACDACE90,
(3)当点D在线段CB的延长线上时,α=β.
理由:∵∠DAE=∠BAC,
∴∠DAB=∠EAC,
∵在△ADB和△AEC中,
AD=AE,∠DAB=∠EAC,AB=AC,
∴△ADB≌△AEC(SAS),
∴∠ABD=∠ACE,
∵∠ABD=∠BAC+∠ACB,∠ACE=∠BCE+∠ACB,
∴∠BAC=∠BCE,
即α=β.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】把下列各数分别填在相应的括号内.
-![]() ,0,0.16,3
,0,0.16,3![]() ,
, ![]() ,-
,-![]() ,
, ![]() ,
,![]() ,-
,-![]() ,-3.14
,-3.14
有理数:{____________________________________________________};
无理数:{____________________________________________________};
负实数:{____________________________________________________}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、D把一个400米的环形跑道分成相等的4段,即两条直道和两条弯道的长度相同.甲平均每秒跑4米,乙平均每秒跑6米,若甲、乙两人分别从A、C两处同时相向出发(如图),当他们第4次相遇时,其相遇点在____________段(填”AB”或”BC”或”CD”或”DA”).
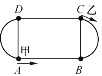
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则A2017的坐标是 . 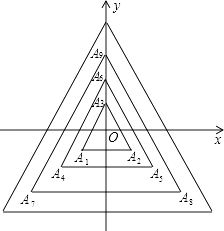
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)△ABC与△A′B′C′在平面直角坐标系中的位置如图.

(1)分别写出下列各点的坐标:A′ ; B′ ;C′ ;
(2)说明△A′B′C′由△ABC经过怎样的平移得到? .
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(4)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+4的图象经过点(-3,-2).
(1)求这个函数的解析式;
(2)画出该函数的图象;
(3)判断点(3,5)是否在此函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
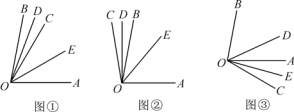
【题目】如图①,已知∠AOB=80°,OC是∠AOB内的一条射线,OD,OE分别平分∠BOC和∠COA.
(1)求∠DOE的度数;
(2)当射线OC绕点O旋转到OB的左侧时如图②(或旋转到OA的右侧时如图③),OD,OE仍是∠BOC和∠COA的平分线,此时∠DOE的大小是否和(1)中的答案相同?若相同,请选取一种情况写出你的求解过程;若不相同,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com