
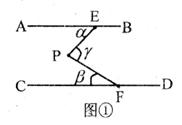
如图所示,平面内,AB∥CD,点E、F分别在直线AB、CD上,点P是这两条直线外的一个动点,连接EP、FP,设∠AEP=∠ ,∠CFP=∠
,∠CFP=∠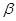 ,∠EPF=∠
,∠EPF=∠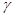 。
。

(1)如果点P在直线AB、CD之间,那么∠ 、∠
、∠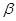 、∠
、∠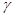 之间有怎样的数量关系(以图①为例)?并说明理由。
之间有怎样的数量关系(以图①为例)?并说明理由。
(2)在(1)中的条件下,请画出符合条件的其他图形(每一种位置只画一个示意图),并直接写出∠ 、∠
、∠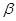 、∠
、∠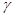 之间的数量关系。(提示:对点P与直线EF的位置关系进行讨论)
之间的数量关系。(提示:对点P与直线EF的位置关系进行讨论)
(3)如果点P在直线AB上方,请画出所有符合题意的图形(每一种位置只画一个示意图),并探索∠ 、∠
、∠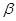 、∠
、∠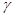 之间的数量关系,选一种图形说明理由。
之间的数量关系,选一种图形说明理由。
(1)∠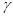 =∠
=∠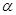 +∠
+∠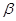 ;(2)当点P在EF的右侧时,有∠
;(2)当点P在EF的右侧时,有∠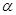 +∠
+∠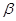 +∠
+∠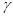 =360°,当点P在EF上时,有∠
=360°,当点P在EF上时,有∠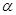 +∠
+∠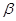 +∠
+∠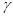 =360°或∠
=360°或∠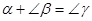 (答对一种即可);(3)三种情况,答案不唯一.
(答对一种即可);(3)三种情况,答案不唯一.
【解析】
试题分析:(1)过点P作PM∥AB,由AB∥CD可得 PM∥CD,根据平行线的性质可得∠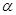 =∠1,∠
=∠1,∠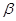 =∠2,由∠
=∠2,由∠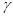 =∠1+∠2即可得到结果;
=∠1+∠2即可得到结果;
(2)分点P在EF的右侧时,当点P在EF上时,两种情况结合平行线的性质分析即可;
(3)先根据题意分析得到有三种位置的图形,选图④说明理由:根据平行线的性质可得 ,再根据
,再根据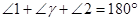 =
=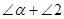 ,即可得到结果.
,即可得到结果.
(1)∠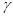 =∠
=∠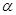 +∠
+∠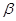 ,理由如下:
,理由如下:
如图,过点P作PM∥AB,
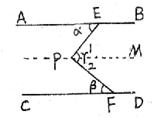
而AB∥CD,则PM∥CD
∴∠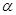 =∠1,∠
=∠1,∠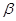 =∠2
=∠2
又∵∠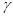 =∠1+∠2
=∠1+∠2
∴∠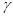 =∠
=∠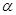 +∠
+∠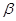
(2)i)当点P在EF的右侧时,如图②,有∠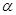 +∠
+∠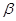 +∠
+∠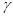 =360°
=360°

ii)当点P在EF上时,如图③,有∠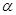 +∠
+∠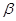 +∠
+∠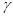 =360°或∠
=360°或∠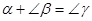 (答对一种即可)
(答对一种即可)
(3)有以下三种位置的图形:


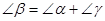
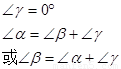
选图④说明理由:
∵AB∥CD
∴
∵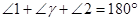 =
=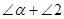
∴
∴ (等量代换).
(等量代换).
考点:平行线的性质的应用
点评:解题的关键是读懂题意及图形,正确作出辅助线,利用平行线的性质解题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
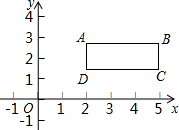 如图所示,平面内有四个点,它们的坐标分别是A(2,2
如图所示,平面内有四个点,它们的坐标分别是A(2,2| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….
如图所示,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,平面内有四个点A,B,C,D,按下列语句画出图形.
如图所示,平面内有四个点A,B,C,D,按下列语句画出图形.查看答案和解析>>
科目:初中数学 来源:2012-2013学年江西省吉安市朝宗实验学校七年级下学期第一次段考数学试卷(带解析) 题型:解答题
如图所示,平面内,AB∥CD,点E、F分别在直线AB、CD上,点P是这两条直线外的一个动点,连接EP、FP,设∠AEP=∠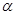 ,∠CFP=∠
,∠CFP=∠ ,∠EPF=∠
,∠EPF=∠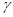 。
。
(1)如果点P在直线AB、CD之间,那么∠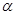 、∠
、∠ 、∠
、∠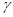 之间有怎样的数量关系(以图①为例)?并说明理由。
之间有怎样的数量关系(以图①为例)?并说明理由。
(2)在(1)中的条件下,请画出符合条件的其他图形(每一种位置只画一个示意图),并直接写出∠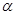 、∠
、∠ 、∠
、∠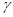 之间的数量关系。(提示:对点P与直线EF的位置关系进行讨论)
之间的数量关系。(提示:对点P与直线EF的位置关系进行讨论)
(3)如果点P在直线AB上方,请画出所有符合题意的图形(每一种位置只画一个示意图),并探索∠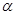 、∠
、∠ 、∠
、∠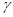 之间的数量关系,选一种图形说明理由。
之间的数量关系,选一种图形说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com