
【题目】在正方形ABCD中,对角线AC与BD交于点O;在Rt△PMN中,∠MPN=90°.
(1)如图1,若点P与点O重合且PM⊥AD、PN⊥AB,分别交AD、AB于点E、F,请直接写出PE与PF的数量关系;
(2)将图1中的Rt△PMN绕点O顺时针旋转角度α(0°<α<45°).
①如图2,在旋转过程中(1)中的结论依然成立吗?若成立,请证明;若不成立,请说明理由;
②如图2,在旋转过程中,当∠DOM=15°时,连接EF,若正方形的边长为2,请直接写出线段EF的长;
③如图3,旋转后,若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP时,猜想此时PE与PF的数量关系,并给出证明;当BD=mBP时,请直接写出PE与PF的数量关系.
【答案】
(1)
解:PE=PF,理由:
∵四边形ABCD为正方形,
∴∠BAC=∠DAC,又PM⊥AD、PN⊥AB,
∴PE=PF
(2)
解:①成立,理由:
∵AC、BD是正方形ABCD的对角线,
∴OA=OD,∠FAO=∠EDO=45°,∠AOD=90°,
∴∠DOE+∠AOE=90°,
∵∠MPN=90°,
∴∠FOA+∠AOE=90°,
∴∠FOA=∠DOE,
在△FOA和△EOD中,
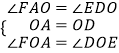 ,
,
∴△FOA≌△EOD,
∴OE=OF,即PE=PF;
②作OG⊥AB于G,
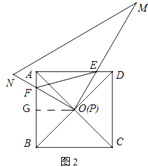
∵∠DOM=15°,
∴∠AOF=15°,则∠FOG=30°,
∵cos∠FOG= ![]() ,
,
∴OF= ![]() =
= ![]() ,又OE=OF,
,又OE=OF,
∴EF= ![]() ;
;
③PE=2PF,
证明:如图3,过点P作HP⊥BD交AB于点H,
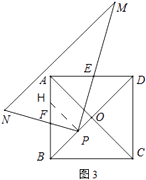
则△HPB为等腰直角三角形,∠HPD=90°,
∴HP=BP,
∵BD=3BP,
∴PD=2BP,
∴PD=2 HP,
又∵∠HPF+∠HPE=90°,∠DPE+∠HPE=90°,
∴∠HPF=∠DPE,
又∵∠BHP=∠EDP=45°,
∴△PHF∽△PDE,
∴ ![]() =
= ![]() =
= ![]() ,
,
即PE=2PF,
由此规律可知,当BD=mBP时,PE=(m﹣1)PF.
【解析】(1)根据正方形的性质和角平分线的性质解答即可;(2)①根据正方形的性质和旋转的性质证明△FOA≌△EOD,得到答案;②作OG⊥AB于G,根据余弦的概念求出OF的长,根据勾股定理求值即可;③过点P作HP⊥BD交AB于点H,根据相似三角形的判定和性质求出PE与PF的数量关系,根据解答结果总结规律得到当BD=mBP时,PE与PF的数量关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
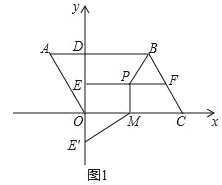
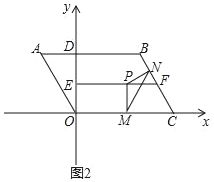
【题目】如图1,已知平行四边形ABCO,以点O为原点,OC所在的直线为x轴,建立直角坐标系,AB交y轴于点D,AD=2,OC=6,∠A=60°,线段EF所在的直线为OD的垂直平分线,点P为线段EF上的动点,PM⊥x轴于点M点,点E与E′关于x轴对称,连接BP、E′M.
(1)请直接写出点A的坐标为_____,点B的坐标为_____;
(2)当BP+PM+ME′的长度最小时,请直接写出此时点P的坐标为_____;
(3)如图2,点N为线段BC上的动点且CM=CN,连接MN,是否存在点P,使△PMN为等腰三角形?若存在,请求出所有满足要求的EP的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点. 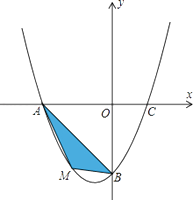
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“幸”、“福”、“聊”、“城”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“福”的概率为多少?
(2)小颖从中任取一球,记下汉字后放回袋中,然后再从中任取一球,求小颖取出的两个球上汉字恰能组成“幸福”或“聊城”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习代数式的值时,介绍了计算程序中的框图:用“![]() ”表示数据输入、输出框;用“
”表示数据输入、输出框;用“![]() ”表示数据处理和运算框;用“
”表示数据处理和运算框;用“![]() ”表示数据判断框(根据条件决定执行两条路径中的某一条).按图所示的程序计算(输入的
”表示数据判断框(根据条件决定执行两条路径中的某一条).按图所示的程序计算(输入的![]() 为正整数).
为正整数).
例如:输入![]() ,结果依次为
,结果依次为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,即运算循环
,即运算循环![]() 次(第
次(第![]() 次计算结果为
次计算结果为![]() )结束.
)结束.
(1)输入![]() ,结果依次为
,结果依次为![]() 、___________________、
、___________________、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
(依次填入循环计算所缺的几次结果)
(2)输入![]() ,运算循环__________次结束.
,运算循环__________次结束.
(3)输入正整数![]() ,经过
,经过![]() 次运算结束,试求
次运算结束,试求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k≠0)的图象与x轴的交点坐标为(-2,0),则下列说法:①y随x的增大而减小;②关于x的方程kx+b=0的解为x=-2;③kx+b>0的解集是x>-2;④b<0.其中正确的有__________.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图中给出的信息,解答下列问题:

(1)放入一个小球水面升高 ,![]() ,放入一个大球水面升高
,放入一个大球水面升高 ![]() ;
;
(2)如果要使水面上升到50![]() ,应放入大球、小球各多少个?
,应放入大球、小球各多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是边长分别为4 ![]() 和2的两个等边三角形纸片ABC和OD′E′叠放在一起(C与O重合).
和2的两个等边三角形纸片ABC和OD′E′叠放在一起(C与O重合). 
(1)操作:固定△ABC,将△ODE绕点C顺时针旋转30°,后得到△ODE,连接AD、BE、CE的延长线交AB于F(图2): 探究:在图2中,线段BE与AD之间有怎样的大小关系?试证明你的结论.
(2)在(1)的条件下将△ODE,在线段CF上沿着CF方向以每秒1个单位的速度平移,平移后的△CDE设为△PQR,当点P与点F重合时停止运动(图3). 探究:设△PQR移动的时间为x秒,△PQR与△ABC重叠部分的面积为y,求y与x之间的函数解析式,并写出函数自变量x的取值范围.
(3)将图1中△ODE固定,把△ABC沿着OE方向平移,使顶点C落在OE的中点G处,设为△ABG,然后奖△ABG绕点G顺时针旋转,边BG交边DE于点M,边AG交边DO于点N,设∠BGE=α(30°<α<90°)(图4). 探究:在图4中,线段ONEM的值是否随α的变化而变化?如果没有变化,请你求出ONEM的值,如果有变化,请你说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com