
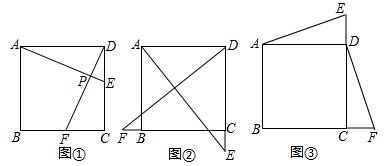
���� ��1����֤�á�ADE�ա�DCF����ȫ�������ε����ʵ�AE=DF����DAE=��CDF�����ɵȽǵ������ȿɵ�AE��DF��
��2���������ε����ʵó�AD=DC����ADE=��DCF=90�㣬DE=CF��SAS֤����ADE�ա�DCF���ó�AE=DF����DAE=��CDF��֤����DAE+��ADF=90�㣬�ó�AE��DF��
��3���ɣ�1��ͬ����֤AE=DF����DAE=��CDF���ӳ�FD��AE�ڵ�G�����ɵȽǵ������ȿɵ�AE��DF��
��� �⣺��1��AE=DF��AE��DF���������£�
���ı���ABCD�������Σ�
��AD=DC����ADC=��C=90�㣬
�߶���E��F�ֱ��D��C����ͬʱ����������ͬ���ٶ���ֱ��DC��CB���ƶ���
��DE=CF��
�ڡ�ADE�͡�DCF�У�$\left\{\begin{array}{l}{AD=DC}&{\;}\\{��ADC=��C}&{\;}\\{DE=CF}&{\;}\end{array}\right.$��
���ADE�ա�DCF��SAS����
��AE=DF����DAE=��CDF��
���ڡ�CDF+��ADF=90�㣬
���DAE+��ADF=90�㣬
���APD=90�㣬
��AE��DF��
�ʴ�Ϊ��AE=DF��AE��DF��
��2��AE=DF��AE��DF���������£�
���ı���ABCD�������Σ�
��AD=DC����ADC=��DCF=90�㣬
�߶���E��F�ֱ��D��C����ͬʱ����������ͬ���ٶ���ֱ��DC��CB���ƶ���
��DE=CF��
�ڡ�ADE�͡�DCF�У�$\left\{\begin{array}{l}{AD=DC}&{\;}\\{��ADC=��DCF}&{\;}\\{DE=CF}&{\;}\end{array}\right.$��
���ADE�ա�DCF��SAS����
��AE=DF����DAE=��CDF��
���ڡ�CDF+��ADF=90�㣬
���DAE+��ADF=90�㣬
��AE��DF��
��3��AE��DF���������£�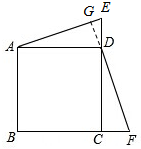 ͬ��1���ã�AE=DF����DAE=��CDF��
ͬ��1���ã�AE=DF����DAE=��CDF��
�ӳ�FD��AE�ڵ�G����ͼ��ʾ��
���CDF+��ADG=90�㣬
���ADG+��DAE=90�㣬
���AGD=90�㣬
��AE��DF��
���� �������ı����ۺ���Ŀ�������������ε����ʡ�ȫ�������ε��ж������ʡ��������ǵĹ�ϵ�����ߵ�֤����֪ʶ�������ѶȽϴ��ۺ���ǿ���������������ε����ʣ�֤��������ȫ���ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Խ���ƽ��һ��Խ� | B�� | �Խ����ഹֱƽ�� | ||
| C�� | �Խ������ | D�� | ��������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com