练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．计算：|-$\sqrt{3}$|-（$\sqrt{2017}$-$\sqrt{2016}$）0-2cos30°+（$\frac{1}{2}}$）-2．

    分析 先根据绝对值、负整数指数幂、特殊角的三角函数值及0指数幂把原式化简，再根据实数混合运算的法则进行计算即可．

    解答 解：原式=$\sqrt{3}-1-2×\frac{{\sqrt{3}}}{2}+4$，
    =$\sqrt{3}-1-\sqrt{3}+4$，
    =3．

    点评 本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟记特殊角的三角函数值，熟练掌握负整数指数幂、零指数幂及绝对值等考点的运算．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    16．在网络上搜索“快乐大本营“能搜索到与之相关的结果约为9480000个，将9480000用科学记数法表示为9.48×106．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．计算：（-$\frac{1}{2}$）-2+2cos60°-20170．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．如图，在△ABC中，AC=3cm，∠ACB=90°，∠ABC=60°，将△ABC绕点B顺时针旋转至△A′BC′，点C′在直线AB上，则边AC扫过区域（图中阴影部分）的面积为3π 　cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，?ABCD中，E、F在AC上，四边形DEBF是平行四边形，求证：AE=CF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．在直角坐标系中，点A，B，C，D的坐标依次为（-1，0），（x，y），（-1，5），（w，z），要使四边形ABCD为平行四边形，则x，y，w，z的值需满足什么条件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

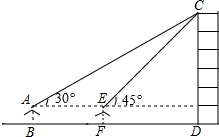    18．某数学兴趣小组在学习了《锐角三角函数》以后，开展测量物体高度的实践活动，测量一建筑物CD的高度，他们站在B处仰望楼顶C，测得仰角为30°，再往建筑物方向走20m，到达点F处测得楼顶C的仰角为45°（BFD在同一直线上）．已知观测员的眼睛与地面距离为1.5m（即AB=1.5m），求这栋建筑物CD的高度．（参考数据：$\sqrt{3}$≈1.732，$\sqrt{2}$≈1.414．结果保留整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如何在一个三角形内部画一个内接正方形？小聪对其进行如下探索：
    第1步：如图1，在△ABC内部先作一个正方形DEFG，使得EF落在BC边上，D落在AB边上，他认为作这样的正方形比较容易实现，但是该正方形顶点G并没有落在AC边上；
    第2步：他认为只要将正方形DEFG逐渐放大，就会实现点G落在AC边上的目的，于是他作了射线BG，交AC于点N；
    第3步：他认为只要点N确定了，那么正方形NQPM就很容易得到了，于是就实现了在三角形内部画一个内接正方形的目的了．
    借鉴小聪的探索过程，请你利用图2和图3，在扇形AOB内部作两个不同类型的内接正方形，并指出上述画图中主要利用了什么样的几何变换？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图放置的正方形ABCD，正方形DCC1D1，正方形D1C1C2D2，…都是边长为$\sqrt{3}$的正方形，点A在y轴上，点B，C，C1，C2，…，都在直线y=$\frac{\sqrt{3}}{3}$x上，则D的坐标是（$\sqrt{3}$，1+$\frac{4\sqrt{3}}{3}$），Dn的坐标是（$\sqrt{3}$（n+1），$\frac{3（n+1）+4\sqrt{3}}{3}$）．

    查看答案和解析>>

    同步练习册答案