
已知:如图所示,在![]() ABCD中,BC=2AB,将AB两端延长,并截取AE=AB=BF,CE交AD于G,DF交CB于H.你能判断CG与DH的位置关系吗?
ABCD中,BC=2AB,将AB两端延长,并截取AE=AB=BF,CE交AD于G,DF交CB于H.你能判断CG与DH的位置关系吗?

|
解:CG与DH互相垂直平分,理由是: 由 又AB=AE,于是AE=CD,又∠1=∠2,∠3=∠CDG 所以△AEG≌△DCG,从而AG=DG= 同理BH=CH= 又DG∥CH,所以四边形DGHC为平行四边形 又CD=DG,可知四边形DGHC为菱形 所以CG与DH互相垂直平分. 解析:由图可知,CG与DH是四边形DGHC的两条对角线.要确定CG与DH的位置关系,关键是确定四边形DGHC是什么图形. 说明:此题先判断四边形DGHC是平行四边形,再说明它的邻边相等,从而判定是菱形. |


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:阅读理解
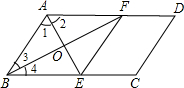 阅读下述说明过程,讨论完成下列问题:
阅读下述说明过程,讨论完成下列问题:| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
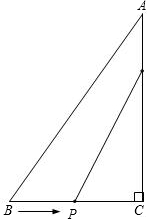 同时出发,其中点P以1厘米/秒的速度沿着线段BC向点C运动,点Q以2厘米/秒的速度沿着线段CA向点A运动.
同时出发,其中点P以1厘米/秒的速度沿着线段BC向点C运动,点Q以2厘米/秒的速度沿着线段CA向点A运动.查看答案和解析>>
科目:初中数学 来源: 题型:
| m | x |
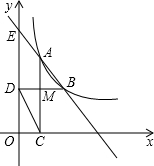 点M,连接DC.
点M,连接DC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com