
| 树苗 | 每株树苗批发价格(元) | 两年后每株树苗对空气的净化指数 |
| 雪松 | 30 | 0.4 |
| 香樟 | 20 | 0.1 |
| 垂柳 | P | 0.2 |
分析 (1)根据购买雪松、香樟、垂柳是总数=400列出方程即可解决.
(2)设购买树苗的总费用为w元,写出w关于x的函数表达式,再求出自变量取值范围,即可解决问题.
(3)构建二次函数利用二次函数的性质解决最值问题.
解答 解:(1)由题意2x+y=400,y=-2x+400.
(2)设购买树苗的总费用为w元,
由题意w=30x+20x+30y=50x+30(-2x+400)=-10x+12000.
因为这400株树苗两年后对该住宅小区的空气净化指数不低于90,
所以0.4x+0.1x+0.2y≥90,
∴0.5x+0.2(-2x+400)≥90,
∴x≥100,
又2x≤400,
∴x≤200,
∴100<x≤200
∵w=-10x+12000,w随x增大而减小,
∴x=200时,w最小=10000元.
(3)由题意W=30x+20x+(30-0.05y)•y=-0.2x2+70x+4000,
∵a=-0.2<0,
∴W有最大值=10125,
∴购买树苗总费用的最大值10125元.
点评 本题考查一次函数的应用,二次函数的性质等知识,解题的关键是构建一次函数或二次函数解决问题,学会利用二次函数的性质解决问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
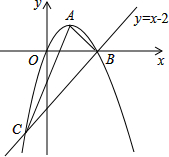 如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x-2交于B,C两点.
如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x-2交于B,C两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ② | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -4的平方根是±2 | |
| B. | 任何数的平方是非负数,因而任何数的平方根也是非负数 | |
| C. | 任何一个非负数的平方根都不大于这个数 | |
| D. | 2是4的算术平方根 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com