
【题目】计算:
(1) (-8)-47+18-(-27)
(2)-![]() ;
;
(3)12-(-18)+(-7)-15;
(4)4.7-(-8.9)-7.5+(-6);
(5)(4![]() ;
;
(6)![]()
科目:初中数学 来源: 题型:
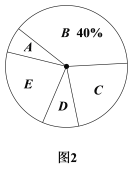
【题目】为调查市民上班时最常用的交通工具的情况,随机抽取了四市部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭轿车,E:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成不完整的条形统计图(图1)和扇形统计图(图2),请结合统计图回答下列问题:
(1)在这次调查中,一共调查了 名市民;
(2)扇形统计图中,C组的百分率是 ;并补全条形统计图;
(3)计算四市中10000名市民上班时最常用家庭轿车的有多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华和小明用两张相同的长方形纸做数学实验,先在两条较长的边上各取一点画一条线,沿画线剪开后再对齐,并将其中一部分沿长边平移一定的距离, 阴影表示平移拉开的区域.小华画了一条线段,如图①所示;小明画了一条曲线,如图②所示.
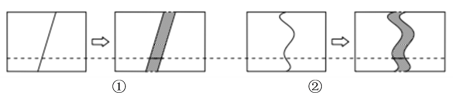
(1)设长方形的长为![]() ,宽为
,宽为![]() ,平移的距离为
,平移的距离为![]() ,请计算两个阴影区域的面积,由计算结果你发现了什么?
,请计算两个阴影区域的面积,由计算结果你发现了什么?
(2)任意画一条与长边平行的直线,被阴影部分所截得的线段是否相等?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李某天的运营全是在东西走向的人民大街进行的,如果规定向东为正,向西为负,他这天下午的行车里程如下(单位:km)
+10、-3、-8、+11、-10、+12、+4、-15、-16、+15
(1)将最后一名乘客送到目的地时,小李距下午出车地点的距离是多少?
(2)若汽车的耗油量为0.5L/㎞,那么这天下午汽车共耗油多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,平行四边形OABC的边OA在x轴的正半轴上,A、C两点的坐标分别为(2,0)、(1,2),点B在第一象限,将直线y=-2x沿y轴向上平移m(m>0)个单位.若平移后的直线与边BC有交点,则m的取值范围是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”期间,某风景区在7天中每天游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化 单位:万人 |
|
|
|
|
|
|
|
(1)若9月30日的游客人数记为![]() ,请用含
,请用含![]() 的代数式表示10月2日的游客人数?
的代数式表示10月2日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由.
(3)此风景区一方面给广大市民提供一个休闲游玩的好去处;另一方面拉动了内需,促进了消费.若9月30日的游客人数为1万人,进园的人每人平均消费60元,问“十一”期间所有游园人员在此风景区的总消费是多少元?(用科学记数法表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环下去.
(1)填写下表:
剪的次数 | 1 | 2 | 3 | 4 | 5 |
正方形个数 | 4 | 7 | 10 |
|
|
(2)如果剪了8次,共剪出 个小正方形.
(3)如果剪n次,共剪出 个小正方形.
(4)设最初正方形纸片为1,则剪n次后,最小正方形的边长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点A(1,0)和B(0,3),其顶点为D.
经过点A(1,0)和B(0,3),其顶点为D.
(1)求此抛物线的表达式;
(2)求△ABD的面积;
(3)设P为该抛物线上一点,且位于抛物线对称轴右侧,作PH⊥对称轴,垂足为H,若△DPH与△AOB相似,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三人准备玩传球游戏.规则是:第1次传球从甲开始,甲先将球随机传给乙、丙两人中的一个人,再由接到球的人随机传给其他两人中的一个人…如此反复.
(1)若传球1次,球在乙手中的概率为 ;
(2)若传球3次,求球在甲手中的概率(用树状图或列表法求解).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com