

分析 (1)根据-2点为A,右移3个单位得到B点为-2+3=1,则可以得出答案;
(2)根据5表示为A点,将点A向左移动7个单位长度,再向右移动5个单位长度,得到点为5-7+5=3,可以得出答案;
(3)根据-6表示为A点,将点A向右移动132个单位长度,再向左移动226个单位长度,得到点为-6+132-226=-100.
解答 解:(1)终点B表示的数是-2+3=1,A,B两点间的距离是:1-(-2)=3;
(2)终点B表示的数是:5-7+5=3,A,B两点间的距离为:5-3=2;
(3)终点B表示的数是-6+132-226=-100,A,B两点间的距离是-6-(-100)=94,
故答案为:(1)1,3;(2)3,2; (3)-100,94.
点评 本题考查了数轴以及有理数的加减运算,注意数形结合的运用,熟知数轴上两点间的距离公式是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
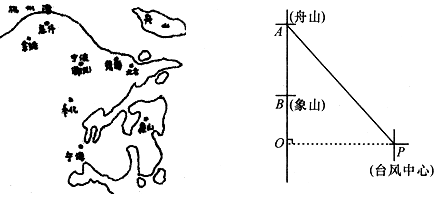
 三角形ABO在平面直角坐标系上如图放置,已知点A(0,10),点B在x轴上,点C在OB上,且AO+OC=AB+BC,BC=2.
三角形ABO在平面直角坐标系上如图放置,已知点A(0,10),点B在x轴上,点C在OB上,且AO+OC=AB+BC,BC=2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 身高180cm和身高90cm | B. | 向东走5公里和向南走5公里 | ||
| C. | 收入300元和支出300元 | D. | 使用汽油10公斤和浪费酒精10公斤 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
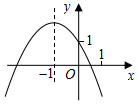 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com