
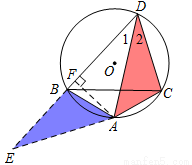
已知:△ABC是⊙O的内接三角形,AB=AC,在∠BAC所对弧AC上,任取一点D,连接AD,BD,CD,
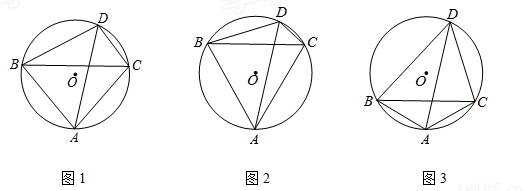
(1)如图1,∠BAC=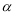 ,直接写出∠ADB的大小(用含
,直接写出∠ADB的大小(用含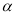 的式子表示);
的式子表示);
(2)如图2,如果 BAC=60°,求证:BD+CD=AD;
BAC=60°,求证:BD+CD=AD;
(3)如图3,如果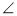 BAC=120°,那么BD+CD与AD之间的数量关系是什么?写出猜测并加以证明.
BAC=120°,那么BD+CD与AD之间的数量关系是什么?写出猜测并加以证明.
(1)∠ADB=90°-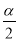 ;(2)证明见试题解析;(3)
;(2)证明见试题解析;(3)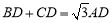 ,证明见试题解析.
,证明见试题解析.
【解析】
试题分析:(1)由AB=AC,得到∠ABC=∠ACB,即可表示出∠ACB=90°-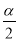 ,再由∠ACB=∠ADB得出结论;
,再由∠ACB=∠ADB得出结论;
(2)延长BD到E,使得DE=DC,可以得到△ABC是等边三角形,再由圆内接四边形的性质,可得到∠BAC=∠EDC=60°,从而有△DCE是等边三角形,由△ACD≌△BCE,得到BE=AD,从而可以得到AD=BD+CD;
(3)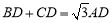 ,延长DB到E,使得BE=DC,连接AE,过点A作AF⊥BD于点F,由等腰三角形的性质和由圆内接四边形的性质,得到∠EBA=∠DCA,故有△EBA≌△DCA,得到∠E=∠1, AE=AD,在Rt△ADF中,解直角三角形可得到
,延长DB到E,使得BE=DC,连接AE,过点A作AF⊥BD于点F,由等腰三角形的性质和由圆内接四边形的性质,得到∠EBA=∠DCA,故有△EBA≌△DCA,得到∠E=∠1, AE=AD,在Rt△ADF中,解直角三角形可得到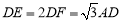 ,从而有
,从而有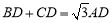 .
.
试题解析:
(1)∠ADB=90°-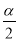 ;
;
(2)延长BD到E,使得DE=DC,∵ BAC=60°,AB=AC,∴△ABC是等边三角形,∴BC=AC,∠BAC=∠ACB=60°,∵四边形ABCD内接于圆,∴∠BAC+∠BDC=180°,∵∠BDC+∠EDC=180°,∴∠BAC=∠EDC=60°,∵DC=DE,∴△DCE是等边三角形,∴∠DCE=60° ,∴∠ACD=∠BCE,∴△ACD≌△BCE,∴BE=AD,∵BE=BD+DE,∴AD=BD+CD;
BAC=60°,AB=AC,∴△ABC是等边三角形,∴BC=AC,∠BAC=∠ACB=60°,∵四边形ABCD内接于圆,∴∠BAC+∠BDC=180°,∵∠BDC+∠EDC=180°,∴∠BAC=∠EDC=60°,∵DC=DE,∴△DCE是等边三角形,∴∠DCE=60° ,∴∠ACD=∠BCE,∴△ACD≌△BCE,∴BE=AD,∵BE=BD+DE,∴AD=BD+CD;
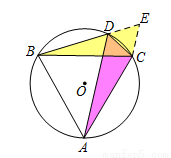
(3)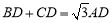 ,证明如下:
,证明如下:
延长DB到E,使得BE=DC,连接AE,过点A作AF⊥BD于点F,∵AB=AC ,∴∠1=∠2,∵四边形ABCD内接于圆,∴∠DBA+∠ACD=180°,∵∠EBA+∠DBA =180°,∴∠EBA=∠DCA,∵BE=CD,AB=AC,∴△EBA≌△DCA,∴∠E=∠1,∴AE=AD,在Rt△ADF中,∠AFD=90°, ∴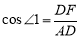 ,∵∠1=90°-
,∵∠1=90°-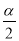 =30°,,∴
=30°,,∴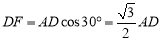 ,∴
,∴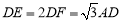 ,∵ BE=BD+CD,∴
,∵ BE=BD+CD,∴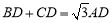 .
.
考点:圆的综合题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源:2014-2015学年黑龙江省五常市九年级上学期12月阶段性测试数学试卷(解析版) 题型:解答题
在△ABC中,AD是BC边上的高,∠B=30°,∠C=45°,CD=2.求BC的长.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省郑州市九年级第一次质量预测数学试卷(解析版) 题型:解答题
如图,△ABC中,BE、CF分别是∠ABC、∠ACB的角平分线,∠A=50°,那么∠BDC的度数是( )
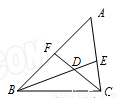
A.105° B.115° C.125° D.135°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省石家庄市九年级上学期第二次月考数学试卷(解析版) 题型:选择题
某商品经过两次降价,由单价100元调至81元,则平均每次降价的百分率是( )
A.8.5﹪ B.9﹪ C.9.5 ﹪ D.10﹪
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市延庆县九年级上学期期末考试数学试卷(解析版) 题型:解答题
某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系: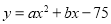 .其图象如图.
.其图象如图.
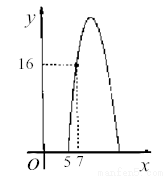
(1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
(2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市延庆县九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,AD是⊙O的直径.
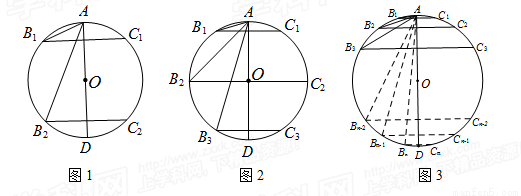
(1)如图1,垂直于AD的两条弦B1C1,B2C2把圆周4等分,则∠B1的度数是 ,∠B2的度数是 ;
(2)如图2,垂直于AD的三条弦B1C1,B2C2,B3C3把圆周6等分,则∠B3的度数是 ;
(3)如图3,垂直于AD的n条弦B1C1,B2C2,B3 C3,…,BnCn把圆周2n等分,则∠Bn的度数是 (用含n的代数式表示∠Bn的度数).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市西城区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,在正方形ABCD中,有一个小正方形EFGH,其中顶点E,F,G分别在AB,BC,FD上.

(1)求证:△EBF∽△FCD;
(2)连接DH,如果BC=12,BF=3,求tan∠HDG的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省心学校九年级上学期数学试卷(解析版) 题型:选择题
已知(5,-1)是双曲线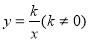 上的一点,则下列各点中不在该图象上的是( )
上的一点,则下列各点中不在该图象上的是( )
A.(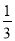 ,-15) B.(5,1) C.(-1,5) D.(10,
,-15) B.(5,1) C.(-1,5) D.(10, )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com