
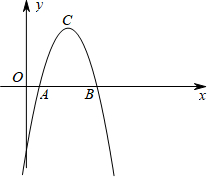
 ��ͼ����֪��x�ύ�ڵ�A��1��0����B��5��0����������l�Ķ���ΪC��3��4����������l���l����x��Գƣ�
��ͼ����֪��x�ύ�ڵ�A��1��0����B��5��0����������l�Ķ���ΪC��3��4����������l���l����x��Գƣ����� ��1�������C������꣬��A��B�����������y=a��x-3��2-4�������������l2�ĺ�����ϵʽ��
��2���ɵ���ƽ�ƹ��ɡ����������ͼ�������Լ�ƽ���ı��εĶԱ���ȵ����ʽ��н��
��3���������֪��M��N����ֱ��x=3�Գƣ�������MNN��M��ı߳�Ϊ2|y0|���ⷽ�����y0���������Ӧ�ĵ�M�����꣮
��� 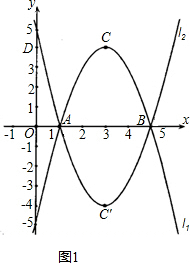 �⣺��1����ͼ1��������֪��C�������Ϊ��3��-4����
�⣺��1����ͼ1��������֪��C�������Ϊ��3��-4����
��l��ĺ�����ϵʽΪy=a��x-3��2-4����1�֣�
����Ϊ��A��1��0����������y=a��x-3��2-4�ϣ�
a��1-3��2-4=0�����a=1��
��������l��ĺ�����ϵʽΪy=��x-3��2-4��y=x2-6x+5��
��2����ͼ2��������ɵã�D��1+m��0����E��5+m��0����F��3+m��-4��
��M��N����ԭ��O�Գƣ�
��OM=ON��
��A��-1-m��0����E��1+m��0����
��A��E����ԭ��O�Գƣ�
��OA=OE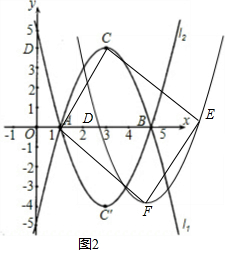
���ı���ANEMΪƽ���ı��Σ�
��AC2=��3-1��2+42=20��
CE2=��5+m-3��2+42=m2+4m+20��
AE2=��5+m-1��2=m2+8m+16��
��AC2+CE2=AE2����20+m2+4m+20=m2+8m+16��
��m=6��
��ʱ��AME��ֱ�������Σ��ҡ�AME=90�㣮
�൱m=6ʱ���Ե�A��C��E��FΪ������ı����Ǿ��Σ�
��3���������������ĵ�M��N���������ߵĶԳ��Կ�֪����M��N����ֱ��x=3�Գƣ�
��M��x0��y0������������MNN��M��ı߳�Ϊ2|y0|��
�ߵ�M��l2�ϣ�
��y0=��3-|y0|-3��2-4��
���y0=$\frac{1��\sqrt{17}}{2}$��
��x0=3-|y0|=$\frac{5-\sqrt{17}}{2}$��$\frac{7-\sqrt{17}}{2}$��
���M��������$\frac{5-\sqrt{17}}{2}$��$\frac{1+\sqrt{17}}{2}$����$\frac{7-\sqrt{17}}{2}$��$\frac{1-\sqrt{17}}{2}$����
���� �����Ƕ��κ������ۺ��⣬�����漰����֪ʶ���������ߵĹ�ʽ����ƽ���ı��κ������ε����ʵ�֪ʶ�㣬�Ǹ����п����ȵ���ѵ㣬����ʱע�����ν�Ϻͷ������۵���ѧ˼������ã�ͬѧ��Ҫ��ǿѵ���������е��⣮


 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10�� | B�� | 9�� | C�� | 8�� | D�� | 7�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | ʱ�� |
| ����ׯ | 9��00 |
| ��ɽ | 12��00 |
| ��ˮ | 14��00 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��֭���� | ̼������ | |
| ���ۣ�Ԫ/�䣩 | 55 | 38 |
| �ۼۣ�Ԫ/�䣩 | 75 | 45 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B�� | $\sqrt{��-2��^{2}}$=-2 | C�� | $\sqrt{8}$=2$\sqrt{2}$ | D�� | $\sqrt{6}$��$\sqrt{3}$=2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij��Ҫ����һ��Բ����ˮ�أ���ˮ�����봹ֱ�ڵ��氲װһ������OA��OǡΪˮ�����ģ����������Ӷ���A������ͷ������ˮ��ˮ���ڸ�������������״��ͬ��������·�����£����ڹ�OA����һƽ���ϣ�������ͼ��ʾ��ƽ��ֱ������ϵʱ��ˮ������ĸ߶�y��m����ˮƽ����x��m��֮��Ĺ�ϵʽ����y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$������������Ϣ���ش��������⣺
ij��Ҫ����һ��Բ����ˮ�أ���ˮ�����봹ֱ�ڵ��氲װһ������OA��OǡΪˮ�����ģ����������Ӷ���A������ͷ������ˮ��ˮ���ڸ�������������״��ͬ��������·�����£����ڹ�OA����һƽ���ϣ�������ͼ��ʾ��ƽ��ֱ������ϵʱ��ˮ������ĸ߶�y��m����ˮƽ����x��m��֮��Ĺ�ϵʽ����y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$������������Ϣ���ش��������⣺�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com