
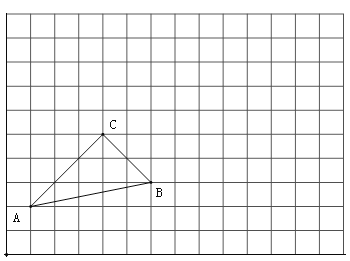
【题目】如图,△ABC是格点三角形(各顶点是网格线的交点), 每个小方格都是边长为1个单位长度的小正方形.
(1)将△ABC向右平移6个单位长度,画出平移后的△A1B1C1.
(2)将平移后的△A1B1C1绕点B1顺时针旋转90°,画出旋转后的△A2B1C2.
(3)将△ABC沿直线BC翻折,画出翻折后的△A3BC.
(4)试问△ABC能否经过一次旋转后与△A2B1C2重合,若能,请在图中用字母O表示旋转中心并写出旋转角的大小;若不能,请说明理由.
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,有个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.
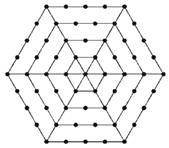
(1)填写下表:
层数 | 1 | 2 | 3 | 4 | 5 | 6 |
该层对应的点数 | 1 | 6 | _____ | 18 | _____ | _____ |
(2)写出第n层所对应的点数为_____;
(3)如果某一层共96个点,那么它是第_____层,此时所有层中共有_____个点.
查看答案和解析>>
科目:初中数学 来源: 题型:
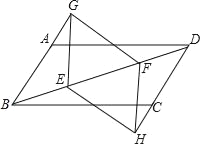
【题目】如图,在ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.
求证:(1)△BEG≌△DFH;
(2)四边形GEHF是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.
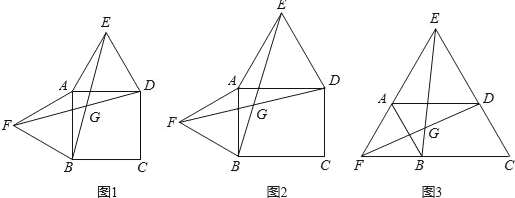
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
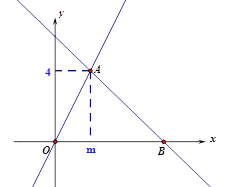
【题目】如图,在平面直角坐标系xOy中,一次函数![]() 的图象与正比例函数
的图象与正比例函数![]() 的图象交于点A(m,4).
的图象交于点A(m,4).
(1)求m、n的值;
(2)设一次函数![]() 的图象与x轴交于点B,求△AOB的面积;
的图象与x轴交于点B,求△AOB的面积;
(3)直接写出使函数![]() 的值小于函数
的值小于函数![]() 的值的自变量x的取值范围.
的值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导“节约用水,从我做起”,鼓楼区政府决定对区直属机关300户家庭的用水情况作一次调查,区政府调查小组随机抽查了其中某些家庭一年的月平均用水量(单位:吨),调查中发现,每户用水量每月均在10﹣14吨范围,并将调查结果制成了如图所示的条形统计图(不完整)和扇形统计图.
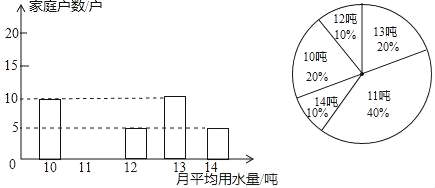
(1)请将条形统计图补充完整;
(2)这些家庭月用水量数据的平均数是 ,众数是 ,中位数是 ;
(3)根据样本数据,估计鼓楼区直属机关300户家庭中月平均用水量不超过12吨的约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB,CD交于点O,将一个三角板的直角顶点放置于点O处,使其两条直角边OE,OF,分别位于OC的两侧.若OC平分∠BOF,OE平分∠COB.
(1)求∠BOE的度数;
(2)写出图中∠BOE的补角,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=2x2的图象与x,y轴分别交于点A,B,与反比例函数y=![]() (x>0)的图象交于点C,且AB=AC,则k的值为()
(x>0)的图象交于点C,且AB=AC,则k的值为()
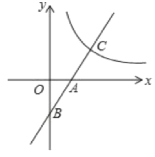
A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境,某化工厂一期工程完成后购买了3台甲型和2台乙型污水处理设备,共花费资金54万元,且每台乙型设备的价格是每台甲型设备价格的75%,实际运行中发现,每台甲型设备每月能处理污水200吨,每台乙型设备每月能处理污水160吨,且每年用于每台甲型设备的各种维护费和电费为1万元,每年用于每台乙型设备的各种维护费和电费为1.5万元.今年该厂二期工程即将完成,产生的污水将大大增加,于是该厂决定再购买甲、乙两型设备共8台用于二期工程的污水处理,预算本次购买资金不超过84万元,预计二期工程完成后每月将产生不少于1300吨污水.
(1)请你计算每台甲型设备和每台乙型设备的价格各是多少元?
(2)请你求出用于二期工程的污水处理设备的所有购买方案;
(3)若两种设备的使用年限都为10年,请你说明在(2)的所有方案中,哪种购买方案的总费用最少?(总费用=设备购买费+各种维护费和电费)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com